题目内容
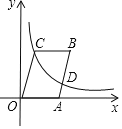
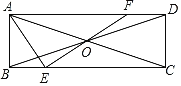
【题目】如图,在矩形ABCD中,AB=1,BC=3,AC和BD交于点O,点E是边BC上的动点(不与点B,C重合),连接EO并延长交AD于点F,连接AE,若△AEF是等腰三角形,则DF的长为_____.
【答案】![]() 或1或
或1或![]() 或
或![]() .
.
【解析】
依据矩形的性质,即可得出△BEO≌△DFO(AAS),进而得到OF=OE,DF=BE.设BE=DF=a,则AF=3-a.当△AEF是等腰三角形时,分三种情况讨论.根据勾股定理列方程即可得到DF的长.
∵四边形ABCD是矩形,
∴AD∥BC,OB=OD,
∴∠FDO=∠EBO,∠DFO=∠BEO,
∴△BEO≌△DFO(AAS),
∴OF=OE,DF=BE.
设BE=DF=a,则AF=3﹣a.
当△AEF是等腰三角形时,分三种情况讨论.
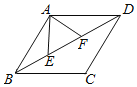
①如图(1),当AE=AF时,在Rt△ABE中,由AE2=AB2+BE2,得(3﹣a)2=12+a2,
解得a=![]()
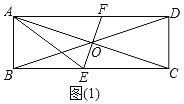
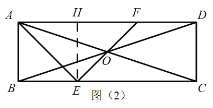
②如图(2),当AE=EF时,过点E作EH⊥AD于点H,则AH=FH=BE,
∴AF=2BE,
∴3﹣a=2a,
解得a=1.
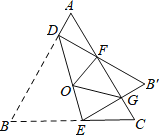
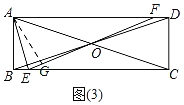
③如图(3),当AF=EF时,∠FAE=∠FEA.
又∠FAE=∠AEB,
∴∠FEA=∠AEB.
过点A作AG⊥EF于点G,则AG=AB=1,EG=BE=a,
∴FG=3﹣2a.
在Rt△AFG中,由AF2=AG2+FG2,得(3﹣a)2=12+(3﹣2a)2,
解得a1=1-![]() , a2=1+
, a2=1+![]() .
.
综上所述,DF的长为![]() 或1或1-
或1或1-![]() 或1+
或1+![]() .
.
故答案为:![]() 或1或1-
或1或1-![]() 或1+
或1+![]() .
.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案【题目】攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)之间的数量满足如下表所示的一次函数关系.
(元/千克)之间的数量满足如下表所示的一次函数关系.
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
(1)某天这种芒果售价为28元/千克.求当天该芒果的销售量
(2)设某天销售这种芒果获利![]() 元,写出
元,写出![]() 与售价
与售价![]() 之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?