题目内容
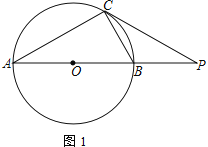
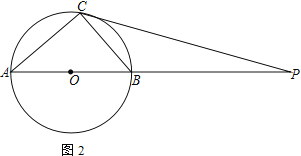
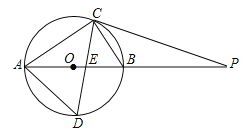
【题目】如图,AB为⊙O的直径,C为⊙O上一点,D、E分别是∠ACB的平分线与⊙O、AB的交点,P为AB延长线上一点,且PC=PE.试判断直线PC与⊙O的位置关系,并说明理由.
【答案】直线PC与⊙O相切.证明见解析.
【解析】试题分析:连结OC,由PC=PE得∠PCE=∠PEC,利用三角形外角性质得∠PEC=∠A+∠ACE=∠A+45°,加上∠A=90°-∠ABC,∠ABC=∠OCB,于是可得到∠PCE=90°-∠OCB+45°=90°-(∠OCE+45°)+45°,则∠OCE+∠PCE=90°,于是根据切线的判定定理可得PC为⊙O的切线
试题解析:直线PC与⊙O相切.
理由:连接OC
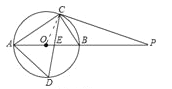
∵PC=PE
∴∠PCE=∠PEC
∴∠PCB+∠BCE=∠ACE+∠CAE
∵CD平分∠ACB
∴∠BCE=∠ACE
∴∠PCB=∠CAE
∵AB为直径
∴∠ACB=90°
∴∠CAE+∠CBA=90°
∴∠PCB+∠CBA=90°
∵OC=OB
∴∠OCB=∠CBA
∴∠PCB+∠OCB =90°,即∠OCP=90°
∴直线PC与⊙O相切.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目