题目内容
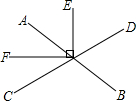
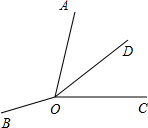
如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=60°,OF⊥OE.
(1)判断OF把∠AOC所分成的两个角的大小关系并证明你的结论;
(2)求∠BOE的度数.
(1)判断OF把∠AOC所分成的两个角的大小关系并证明你的结论;
(2)求∠BOE的度数.

(1)答:∠AOF=∠COF,
证明:∵O是直线CD上一点,
∴∠AOC+∠AOD=180°,
∵∠AOC=60°,
∴∠AOD=180°-60°=120°,
∵OE平分∠AOD,
∴∠AOE=
∠AOD=
×120°=60°.
∵OF⊥OE,
∴∠FOE=90°
∴∠AOF=∠FOE-∠AOE=90°-60°=30°,
∴∠COF=∠AOC-∠AOF=60°-30°=30°,
∴∠AOF=∠COF.
(2)∵∠AOC=60°,
∴∠BOD=∠AOC=60°,∠AOD=180°-60°=120°,
∵OE是∠AOD的平分线,
∴∠DOE=
∠AOD=60°,
∴∠BOE=∠BOD+∠DOE=60°+60°=120°,.
证明:∵O是直线CD上一点,
∴∠AOC+∠AOD=180°,
∵∠AOC=60°,
∴∠AOD=180°-60°=120°,
∵OE平分∠AOD,
∴∠AOE=
| 1 |
| 2 |
| 1 |
| 2 |
∵OF⊥OE,
∴∠FOE=90°
∴∠AOF=∠FOE-∠AOE=90°-60°=30°,
∴∠COF=∠AOC-∠AOF=60°-30°=30°,
∴∠AOF=∠COF.
(2)∵∠AOC=60°,
∴∠BOD=∠AOC=60°,∠AOD=180°-60°=120°,
∵OE是∠AOD的平分线,
∴∠DOE=
| 1 |
| 2 |
∴∠BOE=∠BOD+∠DOE=60°+60°=120°,.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
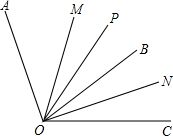
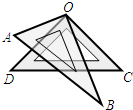
 多少?当∠AOB+∠BOC>180°时,∠MON的度数又是多少?
多少?当∠AOB+∠BOC>180°时,∠MON的度数又是多少?