题目内容
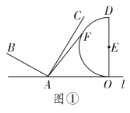
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(4,0),C(0,2)三点.
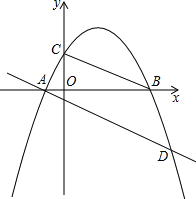
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E,使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
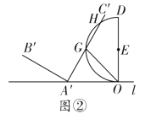
(3)若将直线BC平移,使其经过点A,且与抛物线相交于点D,连接BD,试求出∠BDA的度数.
【答案】(1)抛物线的解析式为:y=-![]() x2+
x2+![]() x+2.(2)存在.E点坐标为(0,2),(3,2).(3)∠ADB=45°.
x+2.(2)存在.E点坐标为(0,2),(3,2).(3)∠ADB=45°.
【解析】
(1)本题需先根据已知条件,过C点,设出该抛物线的解析式为y=ax2+bx+2,再根据过A,B两点,即可得出结果;
(2)由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能是以点E为直角顶点的三角形.由相似关系求出点E的坐标;
(3)如图2,连结AC,作DE⊥x轴于点E,作BF⊥AD于点F,由BC∥AD设BC的解析式为y=kx+b,设AD的解析式为y=kx+n,由待定系数法求出一次函数的解析式,就可以求出点D坐标,由勾股定理就可以求出BD的值,由勾股定理的逆定理就可以得出∠ACB=90°,由平行线的性质就可以得出∠CAD=90°,就可以得出四边形ACBF是矩形,就可以得出BF的值,由勾股定理求出DF的值,而得出DF=BF而得出结论.
(1)∵该抛物线过点C(0,2),
∴可设该抛物线的解析式为y=ax2+bx+2.
将A(-1,0),B(4,0)代入,
得![]()
解得 ,
,
∴抛物线的解析式为:y=-![]() x2+
x2+![]() x+2.
x+2.
(2)存在.
由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能是以点E为直角顶点的三角形.

在Rt△BOC中,OC=2,OB=4,
∴BC=![]() .
.
在Rt△BOC中,设BC边上的高为h,则![]()
∴h=![]() .
.
∵△BEA∽△COB,设E点坐标为(x,y),
∴ ,
,
∴y=±2
将y=2代入抛物线y=-![]() x2+
x2+![]() x+2.
x+2.
得x1=0,x2=3.
当y=-2时,不合题意舍去.
∴E点坐标为(0,2),(3,2).
(3)如图2,连结AC,作DE⊥x轴于点E,作BF⊥AD于点F,

∴∠BED=∠BFD=∠AFB=90°.
设BC的解析式为y=kx+b,由图象,得
![]()
∴
yBC=-![]() x+2.
x+2.
由BC∥AD,设AD的解析式为y=-![]() x+n,由图象,得
x+n,由图象,得
0=-![]() ×(-1)+n
×(-1)+n
∴n=-![]() ,
,
yAD=-![]() x-
x-![]() .
.
∴-![]() x2+
x2+![]() x+2=-
x+2=-![]() x-
x-![]() ,
,
解得:x1=-1,x2=5
∴D(-1,0)与A重合,舍去;
∴D(5,-3).
∵DE⊥x轴,
∴DE=3,OE=5.
由勾股定理,得BD=![]() .
.
∵A(-1,0),B(4,0),C(0,2),
∴OA=1,OB=4,OC=2.
∴AB=5
在Rt△AOC中,Rt△BOC中,由勾股定理,得AC=![]() ,BC=2
,BC=2![]() ,
,
∴AC2=5,BC2=20,AB2=25,
∴AC2+BC2=AB2
∴△ACB是直角三角形,
∴∠ACB=90°.
∵BC∥AD,

∴∠CAF+∠ACB=180°,
∴∠CAF=90°.
∴∠CAF=∠ACB=∠AFB=90°,
∴四边形ACBF是矩形,
∴AC=BF=![]() ,
,
在Rt△BFD中,由勾股定理, 得DF=![]() ,
,
∴DF=BF,
∴∠ADB=45°.

 名校课堂系列答案
名校课堂系列答案【题目】某生产商存有1200千克![]() 产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产
产品,生产成本为150元/千克,售价为400元千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产![]() 产品,
产品,![]() 产品售价为200元/千克.经市场调研发现,
产品售价为200元/千克.经市场调研发现,![]() 产品存货的处理价格
产品存货的处理价格![]() (元/千克)与处理数量
(元/千克)与处理数量![]() (千克)满足一次函数关系(
(千克)满足一次函数关系(![]() ),且得到表中数据.
),且得到表中数据.
|
|
200 | 350 |
400 | 300 |
(1)请求出处理价格![]() (元千克)与处理数量
(元千克)与处理数量![]() (千克)之间的函数关系;
(千克)之间的函数关系;
(2)若![]() 产品生产成本为100元千克,
产品生产成本为100元千克,![]() 产品处理数量为多少千克时,生产
产品处理数量为多少千克时,生产![]() 产品数量最多,最多是多少?
产品数量最多,最多是多少?
(3)由于改进技术,![]() 产品的生产成本降低到了
产品的生产成本降低到了![]() 元/千克,设全部产品全部售出,所得总利润为
元/千克,设全部产品全部售出,所得总利润为![]() (元),若
(元),若![]() 时,满足
时,满足![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围.
的取值范围.