题目内容
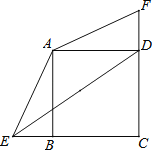
【题目】在正方形ABCD中，BC＝2，E、F分别是CB、CD延长线上的点，DF＝BE，连接AE、AF．
(1)求证：△ADF≌△ABE．
(2)若BE＝1，求sin∠AED的值．
【答案】(1)见解析； (2) 
【解析】
（1）根据正方形的性质可得AB＝DA，∠ABE＝∠ADF＝90°，再根据DF＝BE，即可证明△ADF≌△ABE(SAS)．
（2）作AH⊥DE于H，由勾股定理得DE＝
，AE＝
，根据三角形面积公式求出AH＝
，即可求出sin∠AED的值．
解：（1）∵四边形ABCD是正方形，
∴AB＝BC＝CD＝DA，∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°，
∴∠ABE＝∠ADF＝90°，
在△ADF和△ABE中：
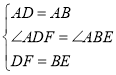
∴△ADF≌△ABE(SAS)．
（2）∵BC＝2，BE＝1，
∴CD＝AD＝AB＝2，CE＝3，
∴DE＝
＝，AE＝
＝，
如图，作AH⊥DE于H，
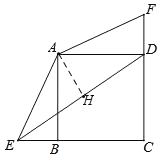
则S△AED＝
DEAH，
又∵S△AED＝ADAB＝2，
∴DEAH＝2，
∴AH＝，
∴sin∠AED＝
＝
．
练习册系列答案
相关题目
