��Ŀ����
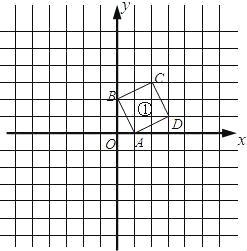
����Ŀ����ƽ��ֱ������ϵ�У���A��1��0����B��0��2����C��2��3����D��3��1�����߶��������������γ�һ��ͼ����ͼ����������ͼ�����Ƶ�O��ʱ����ת90���õ�ͼ�������Ե�OΪλ�����ģ�λ�Ʊ�Ϊ1��2��ͼ������λ�����ĵ������зŴ�õ�ͼ������
��1��������ϵ�зֱ�ͼ������ͼ������
��2������D��ͼ�����ж�Ӧ�ĵ��Ϊ��E����ͼ�����ж�Ӧ�ĵ��Ϊ��F����S��DEF= ��
��3����ͼ��������һ��P��A��B���⣩������Ϊ��a��b����ͼ��������֮��Ӧ�ĵ��Ϊ��Q��ͼ��������֮��Ӧ�ĵ��Ϊ��R����S��PQR= �����ú���a��b�Ĵ���ʽ��ʾ��
���𰸡���1����ͼ�μ���������2��15����3��![]() ��a2+b2��.
��a2+b2��.
��������
�����������1����ͼ�����еĸ������Ƶ�O��ʱ����ת90���õ�֪����Ķ�Ӧ�㣬˳�����Ӷ�Ӧ��õ�ͼ�������Ե�OΪλ�����ģ�λ�Ʊ�Ϊ1��2��ͼ������λ�����ĵ������зŴ�õ�ͼ������������OA��OB��OC��OD�����ӳ���A����B����C����D����ʹOA����OB����OC����OD����OA��OB��OC��OD��2����˳�����Ӹ��㼴�ɣ���2�������������S��DEF�����ļ���ͼ����ɣ����������ʽ���㣮��ͼ�пɿ����������Ǿ��ε���������������ε����������S��DEF=9��5��4��2��2��5��5��2��9��3��2=15����3����������C������P,P��a��b������Q�����꣨-b,a��,R������Ϊ��-2a,-2b��,���ȴ�ͼ���ҳ���������ε����㣬Ȼ����������������Σ��۲�����õ������ε������ʽ=������3�������ε�������г�ʽ�Ӽ��㣮
�����������1����ͼ�����еĸ������Ƶ�O��ʱ����ת90���õ���������Ķ�Ӧ�㣬˳�����Ӷ�Ӧ��õ�ͼ�������Ե�OΪλ�����ģ�λ�Ʊ�Ϊ1��2��ͼ������λ�����ĵ������зŴ�õ�ͼ������������OA��OB��OC��OD�����ӳ���A����B����C����D����ʹOA����OB����OC����OD����OA��OB��OC��OD��2����˳�����Ӹ��㣬��ͼ����ͼ����
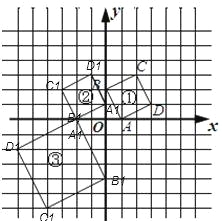
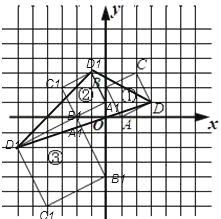
��2����ͼ�пɿ���������DEF������Ǿ��ε���������������ε����������S��DEF=9��5��4��2��2��5��5��2��9��3��2=15����3������P���ڵ�һ�����ڣ�������Ϊ��a��b��������Q������Ϊ��-b��a������R������Ϊ��-2a��-2b����������a��b��S��PQR=��2a+a����a+2b��-![]() (2a-b)(2b+a)-
(2a-b)(2b+a)-![]() (a+b)(a-b)-
(a+b)(a-b)-![]() (2a+a)(2b+b)=3a2+6ab-
(2a+a)(2b+b)=3a2+6ab-![]() (2a2-2b2+3ab+a2-b2+9ab)=3a2+6ab-
(2a2-2b2+3ab+a2-b2+9ab)=3a2+6ab-![]() a2+
a2+![]() b2-6ab=
b2-6ab=![]() ��a2+b2��.
��a2+b2��.

 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�