ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ[Έ Χβ«ιΨ≥]
Έ“Ο«÷ΣΒά ΐ÷α…œΒΡΝΫΒψAΓΔBΒΡΨύάκ|AB|ΘΫ|xAΘ≠xB|Θ§Ρ«Ο¥»γΙϊ“―÷ΣΤΫΟφ…œΝΫΒψP1(x1Θ§y1)Θ§P2(x2Θ§y2)Θ§»γΚΈ«σP1Θ§P2ΒΡΨύάκd(P1P2)ΡΊΘΩ
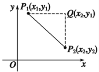
œ¬ΟφΈ“Ο«ΨΆά¥―–ΨΩ’βΗωΈ ΧβΘ°
Έ Χβ “ΜΑψΒΊΘ§“―÷ΣΤΫΟφ…œΝΫΒψP1(x1Θ§y1)Θ§P2(x2Θ§y2)Θ§»γΚΈ«σΒψP1ΚΆP2ΒΡΨύάκΘΩ
¥π:ΓΓΒ±x1ΓΌx2Θ§y1ΘΫy2 ±Θ§|P1P2|ΘΫ|x2Θ≠x1|ΘΜ
Β±x1ΘΫx2Θ§y1ΓΌy2 ±Θ§|P1P2|ΘΫ|y2Θ≠y1|ΘΜ
Β±x1ΓΌx2Θ§y1ΓΌy2 ±Θ§»γΆΦΘ§
‘ΎRtΓςP1QP2÷–Θ§”…Ι¥Ι…Ε®άμ÷ΣΘ§
|P1P2|2ΘΫ|P1Q|2ΘΪ|QP2|2Θ§Υυ“‘d(P1Θ§P2)ΘΫ|P1P2|ΘΫ![]() .
.
ΙιΡ…:ΝΫΒψP1(x1Θ§y1)Θ§P2(x2Θ§y2)ΦδΒΡΨύάκΙΪ Ϋd(P1Θ§P2)ΘΫ|P1P2|ΘΫ![]() .
.
ΫβΨωΈ ΧβΘΚ
Θ®1Θ©“―÷ΣAΘ®2Θ§-4Θ©Θ§BΘ®-2Θ§3Θ©Θ§«σdΘ®A,BΘ©
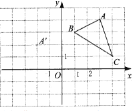
Θ®2Θ©“―÷ΣΒψA(1,2)Θ§B(3,4)Θ§C(5,0)Θ§«σ÷ΛΘΚΓςABC «Β»―ϋ»ΐΫ«–ΈΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©ΦϊœξΫβΘ°
ΘΜΘ®2Θ©ΦϊœξΫβΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©÷±Ϋ”άϊ”ΟΝΫΒψΦδΒΡΨύάκΙΪ ΫΦΤΥψΦ¥Ω…ΘΜ
Θ®2Θ©Ζ÷±π«σ≥ωd(AΘ§B)Θ§d(AΘ§C)Θ§d(CΘ§B)Θ§‘ΌΗυΨίΒ»―ϋ»ΐΫ«–ΈΒΡΕ®“εΦ¥Ω…÷ΛΟςΘ°
ΫβΈωΘΚΘ®1Θ©![]() Θ§
Θ§
Γύ![]() ΘΜ
ΘΜ
Θ®2Θ©÷ΛΟς:ΓΓΓΏ A(1,2)Θ§B(3,4)Θ§C(5,0)Θ§
Γύd(AΘ§B)ΘΫ![]() Θ§
Θ§
d(AΘ§C)ΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
d(CΘ§B)ΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
Γύ|AC|ΘΫ|BC|.
”÷ΓΏΒψAΘ§BΘ§C≤ΜΙ≤œΏΘ§
ΓύΓςABC «Β»―ϋ»ΐΫ«–ΈΘ°

 ΤΎΡ©1ΨμΥΊ÷ ΫΧ”ΐΤάΙάΨμœΒΝ–¥πΑΗ
ΤΎΡ©1ΨμΥΊ÷ ΫΧ”ΐΤάΙάΨμœΒΝ–¥πΑΗ