题目内容
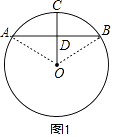
【题目】已知:AB是⊙O的弦,点C是 ![]() 的中点,连接OB、OC,OC交AB于点D.
的中点,连接OB、OC,OC交AB于点D.
(1)如图1,求证:AD=BD; 
(2)如图2,过点B作⊙O的切线交OC的延长线于点M,点P是 ![]() 上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°;
上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°; 
(3)如图3,在(2)的条件下,连接DP、MP,延长MP交⊙O于点Q,若MQ=6DP,sin∠ABO= ![]() ,求
,求 ![]() 的值.
的值. 
【答案】
(1)证明:如图1,连接OA,
∵C是 ![]() 的中点,
的中点,
∴ ![]() ,
,
∴∠AOC=∠BOC,
∵OA=OB,
∴OD⊥AB,AD=BD;
(2)证明:如图2,延长BO交⊙O于点T,连接PT
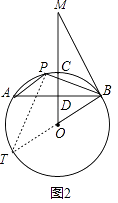
∵BT是⊙O的直径
∴∠BPT=90°,
∴∠APT=∠APB﹣∠BPT=∠APB﹣90°,
∵BM是⊙O的切线,
∴OB⊥BM,
又∠OBA+∠MBA=90°,
∴∠ABO=∠OMB
又∠ABO=∠APT
∴∠APB﹣90°=∠OMB,
∴∠APB﹣∠OMB=90°;
(3)解:如图3,连接MA,
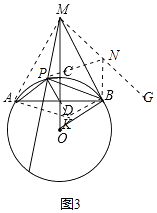
∵MO垂直平分AB,
∴MA=MB,
∴∠MAB=∠MBA,
作∠PMG=∠AMB,
在射线MG上截取MN=MP,
连接PN,BN,
则∠AMP=∠BMN,
∴△APM≌△BNM,
∴AP=BN,∠MAP=∠MBN,
延长PD至点K,
使DK=DP,
连接AK、BK,
∴四边形APBK是平行四边形;
AP∥BK,
∴∠PAB=∠ABK,∠APB+∠PBK=180°,
由(2)得∠APB﹣(90°﹣∠MBA)
=90°,
∴∠APB+∠MBA=180°
∴∠PBK=∠MBA,
∴∠MBP=∠ABK=∠PAB,
∴∠MAP=∠PBA=∠MBN,
∴∠NBP=∠KBP,
∵PB=PB,
∴△PBN≌△PBK,
∴PN=PK=2PD,
过点M作MH⊥PN于点H,
∴PN=2PH,
∴PH=DP,∠PMH=∠ABO,
∵sin∠PMH= ![]() ,sin∠ABO=
,sin∠ABO= ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,设DP=3a,则PM=5a,
,设DP=3a,则PM=5a,
∴MQ=6DP=18a,
∴ ![]() .
.
【解析】(1)如图1,连接OA,利用垂径定理和圆周角定理可得结论;(2)如图2,延长BO交⊙O于点T,连接PT,由圆周角定理可得∠BPT=90°,易得∠APT=∠APB﹣∠BPT=∠APB﹣90°,利用切线的性质定理和垂径定理可得∠ABO=∠OMB,等量代换可得∠ABO=∠APT,易得结论;(3)如图3,连接MA,利用垂直平分线的性质可得MA=MB,易得∠MAB=∠MBA,作∠PMG=∠AMB,在射线MG上截取MN=MP,连接PN,BN,易得△APM≌△BNM,由全等三角形的性质可得AP=BN,∠MAP=∠MBN,延长PD至点K,使DK=DP,连接AK、BK,易得四边形APBK是平行四边形,由平行四边形的性质和平行线的性质可得∠PAB=∠ABK,∠APB+∠PBK=180°,由(2)得∠APB﹣(90°﹣∠MBA)=90°,易得∠NBP=∠KBP,可得△PBN≌△PBK,PN=2PH,利用三角函数的定义可得sin∠PMH= ![]() ,sin∠ABO=
,sin∠ABO= ![]() ,设DP=3a,则PM=5a,可得结果.
,设DP=3a,则PM=5a,可得结果.