题目内容
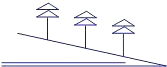如图，在山坡上种树，沿山坡走了10米，高度上升了6米，如果要求树的株距（相邻两棵树之间的水平距离）是4米，那么，斜坡上相邻两棵树之间的坡面距离应是（ ）| A、10米 | B、6米 | C、5米 | D、4米 |
分析：先根据勾股定理求出水平距离，再根据相邻两棵树之间的水平距离是4米列出方程求解．
解答：解：坡面距离就是斜坡的长．沿山坡走了10米，高度上升了6米，由勾股定理可知其水平距离为8米．
设斜坡上相邻两棵树之间的坡面距离是x米，则由题意知
=
，
解得x=5．
故选C
设斜坡上相邻两棵树之间的坡面距离是x米，则由题意知
| 10 |
| 8 |
| x |
| 4 |
解得x=5．
故选C
点评：此题除考查了勾股定理外，还要学生联系实际知道坡面距离就是斜坡的长，也就是直角三角形的斜边，水平距离就是其直角边，所以学生学习时要多联系实际，不可死学．
练习册系列答案
阅读快车系列答案
相关题目
如图，在山坡上种树，要求株距（相邻两树间的水平距离）AC是3米，测得斜坡的倾斜角是30°，则斜坡上相邻两树间的坡面距离AB约是（ ）（保留一位小数，
如图，在山坡上种树，要求株距（相邻两树间的水平距离）是6米，测得斜坡的坡度为1：2.4，则斜坡上相邻两树间的坡面距离是（ ）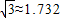
）