题目内容
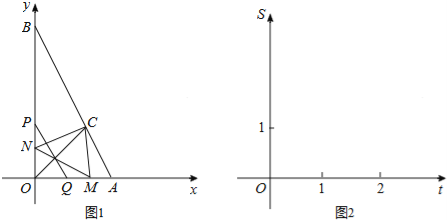
【题目】如图1,已知点A(2,0),B(0,4),∠AOB的平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P、Q关于直线OC的对称点M、N.设P运动的时间为t(0<t<2)秒.
(1)求C点的坐标,并直接写出点M、N的坐标(用含t的代数式表示);
(2)设△MNC与△OAB重叠部分的面积为S.
①试求S关于t的函数关系式;
②在图2的直角坐标系中,画出S关于t的函数图象,并回答:S是否有最大值?若有,写出S的最大值;若没有,请说明理由.
【答案】(1)(![]() ,
,![]() ),P(0,2t),Q(t,0);(2)①
),P(0,2t),Q(t,0);(2)① ;②当t=1时,S有最大值,最大值为1.
;②当t=1时,S有最大值,最大值为1.
【解析】
试题(1)如答图1,作辅助线,由比例式求出点D的坐标;
(2)①所求函数关系式为分段函数,需要分类讨论:答图2,答图3表示出运动过程中重叠部分(阴影)的变化,分别求解.
②画出函数图象,由两段抛物线构成.观察图象,可知当t=1时,S有最大值.
试题解析:解:(1)如答图1,过点C作CF⊥x轴于点F,CE⊥y轴于点E,
由题意,易知四边形OECF为正方形,设正方形边长为x.
∵CE∥x轴,∴△BEC∽△BOA.∴![]() ,即
,即![]() ,解得x=
,解得x=![]() .
.
∴C点坐标为(![]() ,
,![]() ).
).
∵PQ∥AB,∴![]() ,即
,即![]() .
.
∴OP=2OQ.
∵P(0,2t),∴Q(t,0).
∵对称轴OC为第一象限的角平分线,∴对称点坐标为:M(2t,0),N(0,t).
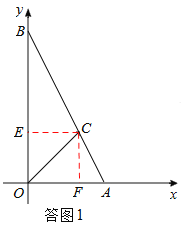
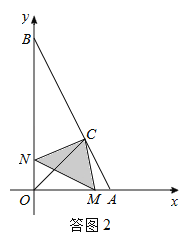
(2)①当0<t≤1时,如答图2所示,点M在线段OA上,重叠部分面积为S△CMN.
S△CMN=S四边形CMON﹣S△OMN=(S△COM+S△CON)﹣S△OMN![]() .
.
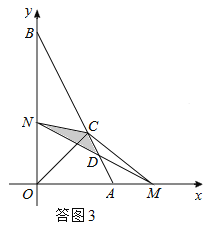
当1<t<2时,如答图3所示,点M在OA的延长线上,
设MN与AB交于点D,则重叠部分面积为S△CDN.
设直线MN的解析式为y=kx+b,
将M(2t,0)、N(0,t)代入得![]() ,解得
,解得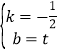 .
.
∴直线MN的解析式为![]() .
.
同理求得直线AB的解析式为:y=﹣2x+4.
联立![]() 与y=﹣2x+4,求得点D的横坐标为
与y=﹣2x+4,求得点D的横坐标为![]() .
.
S△CDN=S△BDN﹣S△BCN=![]() .
.
综上所述,S关于t的函数关系式为 .
.
②画出函数图象,如答图4所示:
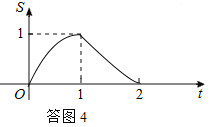
观察图象,可知当t=1时,S有最大值,最大值为1.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率;
(2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由;
(3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.