题目内容

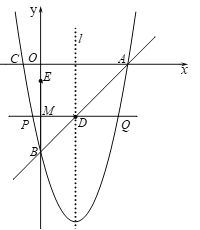
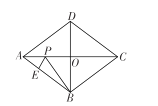
【题目】如图，菱形 的对角线交于点 是线段上一动点， E 是线段 AB上一个动点，则 的最小值为 ____________．

【答案】

【解析】

本题中BP+EP是折线段，要想最小，故想办法将折线段拉直，故过B点作AC的对称点，刚好为D点，连接DP，则发现DP=BP，故相当于求DP+PE的最小值，根据点到直线的距离垂线段最短知：过D点作AB的垂线，交AB于H点，DH即为最小值，再利用菱形等面积法求DH的长.

解：过B点作AC的对称点，由菱形对称性知刚好落在D处，连接DP，

则BP=DP，故BP+EP=DP+EP，

过D点作DH⊥AB于H点，

∴ 当E、P、D三点共线，且DE⊥AB时，由点到直线的距离垂线段最短知：

此时DP+EP有最小值，为DH长.

又四边形ABCD为菱形，DH⊥AB，

∴由菱形的等面积法知：AB×DH=×AC×BD，且AB=5，代入数据：

∴ 5×DH=×8×6，故DH=.

故答案为：.

练习册系列答案
相关题目

【题目】已知抛物线．

（1）求抛物线的开口方向、对称轴和顶点坐标；

（2）将抛物线向下平移，得抛物线，使抛物线的顶点落在直线上．

①求抛物线的解析式；

②抛物线与轴的交点为，（点在点的左侧），抛物线的对称轴于轴的交点为，点是线段上的一点，过点作直线轴，交抛物线于点，点关于抛物线对称轴的对称点为，点是线段上一点，且，连接，作交轴于点，且，求点的坐标．

【题目】在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：

第一步：对折矩形纸片，使与重合，得到折痕，把纸片展开（如图①）；

第二步：再一次折叠纸片，使点落在上，并使折痕经过点，得到折痕，同时得到线段（如图②）．

如图②所示建立平面直角坐标系，请解答以下问题：

（Ⅰ）设直线的解析式为，求的值；

（Ⅱ）若的延长线与矩形的边交于点，设矩形的边，；

（i）若，，求点的坐标；

（ii）请直接写出、应该满足的条件．

【题目】如图，四边形ABCD为矩形，以A为圆心，AD为半径的弧交AB的延长线于点E，连接BD，若AD=2AB=4，则图中阴影部分的面积为______．

【题目】如图，直线分别与轴、轴交于点，抛物线经过点，与轴的另一个交点为，抛物线的对称轴交于点．

（1）求抛物线的函数关系式及对称轴；

（2）若为轴上一动点，为的中点，过点作的中垂线，交抛物线于点，其中在的左边．

①如图1，若时，求的长．

②当以点为顶点的三角形是直角三角形时，请直接写出点的坐标．

【题目】甲、乙二人都是户外运动爱好者，在一次登山活动中，甲、乙二人距出发点的高度 （单位：米）， （单位：米）与乙登山时间 x （单位：分钟）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：

（1）甲登山的速度是每分钟 米，乙在 2 分钟时提速，提速时距地面的高度 为______米；

（2）若乙提速后，乙的速度是甲登山速度的 3 倍，请分别求出甲、乙二人登山全过程中，登山时距地面的高度 ， 与乙登山时间之间的函数关系式；

（3）在（2）的条件下，乙登山多长时间追上了甲? 此时乙距提速时的高度为多少米?

【题目】如图，中，对角线与相交于点点为的中点，连接的延长线交的延长线于点连接．

（1）求证：；

（2）若判断四边形的形状，并证明你的结论．

【题目】如图，在Rt⊿ABC中，∠ACB是直角， tan∠B=,BC=16 cm,点D以2cm/s的速度由点A向点B匀速运动，到达点B即停止，M、N分别是AD、CD的中点，连结MN，设点D的运动时间为t

（1）求MN的长；

（2）求点D由点A到点B匀速运动过程中，线段MN所扫过的面积；

（3）若⊿DMN是等腰三角形时，求t的值．

【题目】南沙群岛是我国固有领土，现在我南海渔民要在南沙某海岛附近进行捕鱼作业，当渔船航行至B处时，测得该岛位于正北方向海里的C处，为了防止某国还巡警干扰，就请求我A处的鱼监船前往C处护航，已知C位于A处的北偏东45°方向上，A位于B的北偏西30°的方向上，求A、C之间的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网