题目内容
已知:如图,∠MAN=30°,O为边AN上一点,以O为圆心、2为半径作⊙O,交AN于D、E两点,设AD=x
。
⑴如图⑴,当x取何值时,⊙O与AM相切;
⑵如图⑵,当x为何值时,⊙O与AM相交于B、C两点,且∠BOC=90°。
。
⑴如图⑴,当x取何值时,⊙O与AM相切;
⑵如图⑵,当x为何值时,⊙O与AM相交于B、C两点,且∠BOC=90°。

| 解:(1)如图⑴,设⊙O与AM相切于C,连结OC, 则∠ACO=90°, ∵∠MAN=30°, ∴OA=2OC, ∵OC=2, ∴OA=4, ∴AD=OA-OD=2, 即当x=2时,⊙O与AM相切; (2)如图⑵,过点O作OG⊥AM于G, 当∠BOC=90°时, ∵OB=OC=2, ∴BC=2 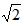 , ,又∵OG⊥BC, ∴G为BC的中点, ∴OG= 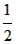 BC= BC=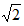 , ,又∵∠A=30°, ∴OA=2 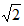 , ,∴AD=2 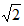 -2, -2,即当x=2 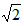 -2时,⊙O与AM相交于B、C两点,且∠BOC=90°。 -2时,⊙O与AM相交于B、C两点,且∠BOC=90°。 |
 |

练习册系列答案
相关题目
 18、已知:如图,∠MAN=45°,B为AM上的一个定点.若点P在射线AN上,以P为圆心,PA为半径的圆与射线AN的另一个交点为C.请确定⊙P的位置,使BC恰与⊙P相切.
18、已知:如图,∠MAN=45°,B为AM上的一个定点.若点P在射线AN上,以P为圆心,PA为半径的圆与射线AN的另一个交点为C.请确定⊙P的位置,使BC恰与⊙P相切. 已知:如图,∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,当AD=
已知:如图,∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,当AD= 22、已知:如图,∠MAN=30°,点O为AN上一点,以O为圆心,2为半径作⊙O,交AN于D、E两点,⊙O与AM相切时,求AD的长.
22、已知:如图,∠MAN=30°,点O为AN上一点,以O为圆心,2为半径作⊙O,交AN于D、E两点,⊙O与AM相切时,求AD的长.
