题目内容
已知：如图，∠MAN=30°，O为边AN上一点，以O为圆心，2为半径作⊙O，交AN于D，E两点，当AD=分析：连接OC，根据切线的判定进行分析即可得到AD的长．
解答：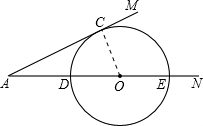
解：如图，设AM切⊙O于点C，连接AC，
则AC⊥OC，
∴∠ACO=90°，OC=OD=2，
∵∠MAN=30°，
∴OC=
OA；
∵OC=OD=2，
∴OA=4，
∴AD=OA-OD=2，
∴当AD=2时，⊙O与AM相切．
故答案为：2．
解：如图，设AM切⊙O于点C，连接AC，则AC⊥OC，
∴∠ACO=90°，OC=OD=2，
∵∠MAN=30°，
∴OC=
| 1 |
| 2 |
∵OC=OD=2，
∴OA=4，
∴AD=OA-OD=2，
∴当AD=2时，⊙O与AM相切．
故答案为：2．
点评：此题考查了圆的切线的性质，圆的切线垂直于过切点的半径；还考查了直角三角形的性质，30°角所对的直角边是斜边的一半．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
18、已知：如图，∠MAN=45°，B为AM上的一个定点．若点P在射线AN上，以P为圆心，PA为半径的圆与射线AN的另一个交点为C．请确定⊙P的位置，使BC恰与⊙P相切．
22、已知：如图，∠MAN=30°，点O为AN上一点，以O为圆心，2为半径作⊙O，交AN于D、E两点，⊙O与AM相切时，求AD的长．
