题目内容
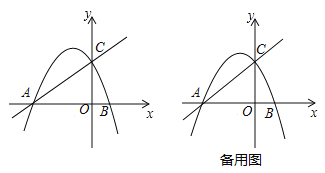
【题目】在直角坐标平面内,直线y=![]() x+2分别与x轴、y轴交于点A、C.抛物线y=﹣
x+2分别与x轴、y轴交于点A、C.抛物线y=﹣![]() +bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
(1)求上述抛物线的表达式;
(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;
(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.
【答案】(1)y=﹣![]() x+2;(2)
x+2;(2)![]() ;(3)(﹣
;(3)(﹣![]() ,
,![]() )或(﹣3,2).
)或(﹣3,2).
【解析】试题分析:(1)由直线得到A、C的坐标,然后代入二次函数解析式,利用待定系数法即可得;
(2)过点E作EH⊥AB于点H,由已知可得![]() ,从而可得
,从而可得![]() 、
、![]() 的长,然后再根据三角函数的定义即可得;
的长,然后再根据三角函数的定义即可得;
(3)分情况讨论即可得.
试题分析:(1)由已知得A(-4,0),C(0,2) ,
把A、C两点的坐标代入![]() 得,
得,
![]() ,∴
,∴ ,
,
∴![]() ;
;
(2)过点E作EH⊥AB于点H,
由上可知B(1,0), ∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ∴
∴![]() ,
,
∵![]() ∴
∴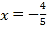 ;
;
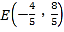
(3)∵DF⊥AC , ∴![]() ,
,
①若![]() ,则CD//AO , ∴点D的纵坐标为2,
,则CD//AO , ∴点D的纵坐标为2,
把y=2代入![]() 得x=-3或x=0(舍去),
得x=-3或x=0(舍去),
∴D(-3,2) ;
②若![]() 时,过点D作DG⊥y轴于点G,过点C作CQ⊥DG交x轴于点Q,
时,过点D作DG⊥y轴于点G,过点C作CQ⊥DG交x轴于点Q,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
设Q(m,0),则![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
易证:![]() ∽
∽![]() ,∴
,∴![]() ,
,
设D(-4t,3t+2)代入![]() 得t=0(舍去)或者
得t=0(舍去)或者![]() ,
,
∴![]() .
.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板:

(1)观察图形,填写下表:
图形 | (1) | (2) | (3) | …… |
黑色瓷砖的块数 | 4 | …… | ||
黑白两种瓷砖的总块数 | 15 | …… |
(2)依上推测,第n个图形中黑色瓷砖的块数为__________________;黑白两种瓷砖的总块数为__________________(都用含n的代数式表示)
(3)白色瓷砖的块数可能比黑色瓷砖的块数多2014块吗?若能,求出是第几个图形;若不能,请说明理由.
【题目】“十一”期间,某风景区在7天中每天游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 单位:万人 |
|
|
|
|
|
|
|
(1)若9月30日的游客人数记为![]() ,请用含
,请用含![]() 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)此风景区一方面给广大市民提供一个休闲游玩的好去处;另一方面拉动了内需,促进了消费.若9月30日的游客人数为1万人,进园的人每人平均消费60元,问“十一”期间所有游园人员在此风景区的总消费是多少元?(用科学记数法表示)