题目内容
已知D是等边△ABC外一点,∠BDC=120º则AD、BD、DC三条线段的数量关系为_____________．
【答案】
AD=BD+DC
【解析】解：延长BD至E，使DE=DC，连接CE．
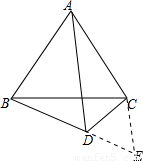
∵∠BDC=120°，
∴∠CDE=60°，又DE=DC，
∴△CDE为等边三角形，
∴CD=DE=CE，∠DCE=60°．
∵△ABC为等边三角形，
∴AC=BC，∠BCA=60°，
∴∠ACB=∠PCE，
∴∠ACB+∠BCD=∠DCE+∠BCD，
即：∠ACD=∠BCE，
∴△ACD≌△BCE，
∴AD=BE，
∵BE=BD+DE，
∴AD=BD+DC．
练习册系列答案
相关题目
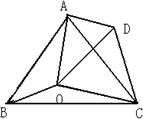16、如图，已知O是等边△ABC内的一点，∠AOB=110°，将△BOC绕点C按顺时针方向旋转60°，得△ADC，连接OD．
已知D是等边△ABC外一点，∠BDC=120°，则AD、BD、DC三条线段的数量关系为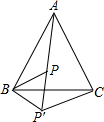
如图，已知P是等边△ABC内的一点，连接AP、BP，将△ABP旋转后能与△CBP′重合，根据图形回答：（1）旋转中心是哪一点？