题目内容
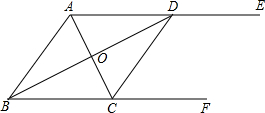 (2012•漳州模拟)如图,AE∥BF,AC平分∠BAE,且交BF于点C,在AE上取一点D,使得AD=BC,连接CD和BD,BD交AC于点O.
(2012•漳州模拟)如图,AE∥BF,AC平分∠BAE,且交BF于点C,在AE上取一点D,使得AD=BC,连接CD和BD,BD交AC于点O.(1)求证:△AOD≌△COB;
(2)求证:四边形ABCD是菱形.
分析:(1)首先根据平行线的性质可得∠DAO=∠BCO,再有条件AD=BC,∠AOD=∠COB,可以利用AAS定理证明△AOD≌△COB;
(2)首先证明四边形ABCD是平行四边形,再证明∠BAC=∠BCA,可利用等角对等边得到AB=BC,即可根据一组邻边相等的平行四边形是菱形证出结论.
(2)首先证明四边形ABCD是平行四边形,再证明∠BAC=∠BCA,可利用等角对等边得到AB=BC,即可根据一组邻边相等的平行四边形是菱形证出结论.
解答:证明:(1)∵AE∥BF,
∴∠DAO=∠BCO,
∵在△AOD和△COB中
,
∴△AOD≌△COB(AAS);
(2)∵AE∥BF,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∵AC平分∠BAD,
∴∠BAC=∠DAC,
∵∠DAO=∠BCO,
∴∠BAC=∠BCA,
∴AB=BC,
∴平行四边形ABCD是菱形.
∴∠DAO=∠BCO,
∵在△AOD和△COB中
|

∴△AOD≌△COB(AAS);
(2)∵AE∥BF,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∵AC平分∠BAD,
∴∠BAC=∠DAC,
∵∠DAO=∠BCO,
∴∠BAC=∠BCA,
∴AB=BC,
∴平行四边形ABCD是菱形.
点评:此题主要考查了全等三角形的判定,菱形的判定,关键是掌握:①全等三角形的判定定理:SSS、SAS、AAS、ASA;②菱形的判定方法:菱形定义:一组邻边相等的平行四边形是菱形;四条边都相等的四边形是菱形;对角线互相垂直的平行四边形是菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•漳州模拟)某几何体的三视图如图所示,则这个几何体是 ( )
(2012•漳州模拟)某几何体的三视图如图所示,则这个几何体是 ( )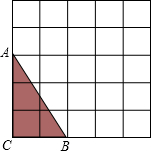 (2012•漳州模拟)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上.
(2012•漳州模拟)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上.