题目内容
(2012•漳州模拟)先化简式子
÷
-
,然后从-2<x≤2中选择一个合适的整数x代入求值.
| x-3 |
| x2-1 |
| x |
| x+1 |
| 1 |
| x-1 |
分析:先把分母因式分解和把除法运算转化为乘法运算得到原式=
•
-
,约分得
-
,再通分进行分式的加减运算得到原式=-
,由于-2<x≤2且x为整数,
则x=-1,0,1,2,而x≠0且x-1)(x+1)≠0,得到x=2,然后把x=2代入计算即可.
| x-3 |
| (x-1)(x+1) |
| x+1 |
| x |
| 1 |
| x-1 |
| x-3 |
| x(x-1) |
| 1 |
| x-1 |
| 3 |
| x2-x |
则x=-1,0,1,2,而x≠0且x-1)(x+1)≠0,得到x=2,然后把x=2代入计算即可.
解答:解:原式=
•
-
=
-
=
-
=-
=-
,
∵-2<x≤2且x为整数,
∴x=-1,0,1,2
∵x(x-1)(x+1)≠0,
∴x≠0且x≠±1,
∴x=2
当x=2时,原式=-
=-
.
| x-3 |
| (x-1)(x+1) |
| x+1 |
| x |
| 1 |
| x-1 |
=
| x-3 |
| x(x-1) |
| 1 |
| x-1 |
=
| x-3 |
| x(x-1) |
| x |
| x(x-1) |
=-
| 3 |
| x(x-1) |
=-
| 3 |
| x2-x |
∵-2<x≤2且x为整数,
∴x=-1,0,1,2
∵x(x-1)(x+1)≠0,
∴x≠0且x≠±1,
∴x=2
当x=2时,原式=-
| 3 |
| 22-2 |
| 3 |
| 2 |
点评:本题考查了分式的化简求值:先把各分式的分子或分母因式分解,再进行约分,接着进行分式的加减运算,得到最简分式或整式(若有括号,先把括号内通分,除法运算转化为乘法运算);然后把满足条件的字母的值代入进行计算得到对应分式的值.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 (2012•漳州模拟)某几何体的三视图如图所示,则这个几何体是 ( )
(2012•漳州模拟)某几何体的三视图如图所示,则这个几何体是 ( )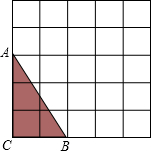 (2012•漳州模拟)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上.
(2012•漳州模拟)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上.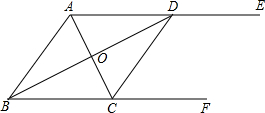 (2012•漳州模拟)如图,AE∥BF,AC平分∠BAE,且交BF于点C,在AE上取一点D,使得AD=BC,连接CD和BD,BD交AC于点O.
(2012•漳州模拟)如图,AE∥BF,AC平分∠BAE,且交BF于点C,在AE上取一点D,使得AD=BC,连接CD和BD,BD交AC于点O.