题目内容
(2012•漳州模拟)已知等腰三角形的两边长为4,8,则第三边的长度是
8
8
.分析:题目给出等腰三角形有两条边长为4和8,而没有明确腰、底分别是多少,所以分两种情况进行讨论,同时利用三角形的三边关系验证能否组成三角形,进而得到答案.
解答:解:由等腰三角形的概念得:
第三边的长可能为4或8,
当第三边是4时,而4+4=8,所以应舍去;
当第三边是8时,而8+8=16>4,能构成三角形;
则第三边长为8.
故答案为:8.
第三边的长可能为4或8,
当第三边是4时,而4+4=8,所以应舍去;
当第三边是8时,而8+8=16>4,能构成三角形;
则第三边长为8.
故答案为:8.
点评:本题考查了等腰三角形的性质和三角形的三边关系,已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,同时要求学生注意验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
相关题目
 (2012•漳州模拟)某几何体的三视图如图所示,则这个几何体是 ( )
(2012•漳州模拟)某几何体的三视图如图所示,则这个几何体是 ( )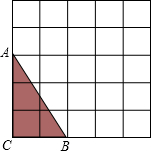 (2012•漳州模拟)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上.
(2012•漳州模拟)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上.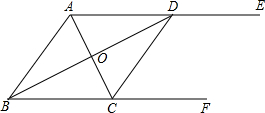 (2012•漳州模拟)如图,AE∥BF,AC平分∠BAE,且交BF于点C,在AE上取一点D,使得AD=BC,连接CD和BD,BD交AC于点O.
(2012•漳州模拟)如图,AE∥BF,AC平分∠BAE,且交BF于点C,在AE上取一点D,使得AD=BC,连接CD和BD,BD交AC于点O.