��Ŀ����
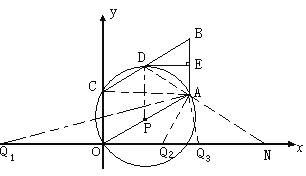
����Ŀ������ͼ14��ʾ��ƽ��ֱ������ϵ�У���C��y����������ϣ��ı���OABCΪƽ���ı��Σ�OA��2����AOC��60�㣬��OAΪֱ���ġ�P������C����BC�ڵ�D��DE��AB����AB��E��
��1�����A��B�����ꣻ
��2����֤��DE�ǡ�P�����ߣ�
(3) С���ڽ����ʱ����������DA���ӳ�����x���ڵ�N�����AON�ǵ��������Σ��ɴˣ����϶�����x����һ�����ڳ���N����ĵ�Q��ʹ��AOQҲ�ǵ��������Σ��ҵ�Qһ���ڡ�P�⡱����ͬ�����Ŀ���������˵�����ɣ�

���𰸡���1��A������Ϊ��![]() ��1����B������Ϊ��
��1����B������Ϊ��![]() ��2����2��֤������������3����ͬ�⡣���ɼ�����.
��2����2��֤������������3����ͬ�⡣���ɼ�����.
�������������������1�����ȵó�����ACO=90�㣬��������OA=2����AOC=60�㣬�ó�OC=1��AC=![]() �����ɵó�A�����꣬��������ƽ���ı��ε����ʵó�B�����ꣻ
�����ɵó�A�����꣬��������ƽ���ı��ε����ʵó�B�����ꣻ
��2�����ȵó��ı���OADCΪ�������Σ������ó���PADΪ�ȱ������Σ��Ӷ��ó���BAD=��PDA���Լ�PD��AB�����ɵó��𰸣�
��3���ֱ���ݢٵ�OA=OQʱ���ڵ�OQ=AQʱ���Q�����꼴�ɣ�
���������
��1���⣺����AC��
�ߡ�OAΪ��P��ֱ����
�ࡡ��ACO��90�㣬
�֡ߡ�OA��2����AOC��60�㣬
�ࡡOC��1��AC��![]() ��
��
�ࡡA������Ϊ��![]() ��1����
��1����
�ߡ�OABCΪƽ���ı��Σ�
�ࡡAB��OC��
�ࡡB������Ϊ��![]() ��2����
��2����
��2��֤��������PD��AD����ͼ��ʾ��
���ı���OABC��ƽ���ı��Σ�
��CD��OA��
�OC����AD��
��OC��AD��
���ı���OADCΪ�������Σ�
���DAO����AOC��60�㣬
��PA��PD��
���PADΪ�ȱ������Σ�
���PDA��60�㣬
�ߡ�BAO��180�㣭60�㣽120�㣬��DAO��60�㣬
���BAD��60�㣬��
���BAD����PDA��
��PD��AB��
��DE��AB��
��DE��PD����
��DE�ǡ�P�����ߡ�
��3���⣺��ͬ�⡣��������:��
�ٵ�OA=OQʱ��
�Ե�OΪԲ�ģ�OAΪ�뾶������x����Q1��Q3���㣬
�õ�Q1����2,0����Q3��2��0��
�ڵ�OQ=AQʱ����OA���д��ߣ���x���ڵ�Q2��
OQ2��![]() ��
��![]() ����Q2��
����Q2��![]() ��0����
��0����
��ˣ���x���ϣ�����N���⣬�ȴ��ڡ�P�ڵĵ�Q2���ִ��ڡ�P��ĵ�Q1��Q3�����Ƿֱ�ʹ��AOQΪ���������Ρ�