题目内容
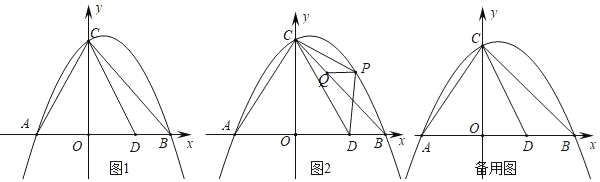
【题目】如图1,抛物线与y=﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点D是线段AB上一点,且AD=CA,连接CD.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点D是线段AB上一点,且AD=CA,连接CD.
(1)如图2,点P是直线BC上方抛物线上的一动点,在线段BC上有一动点Q,连接PC、PD、PQ,当△PCD面积最大时,求PQ+![]() CQ的最小值;
CQ的最小值;
(2)将过点D的直线绕点D旋转,设旋转中的直线l分别与直线AC、直线CO交于点M、N,当△CMN为等腰三角形时,直接写出CM的长.
【答案】(1)![]() ;(2)CM的长为
;(2)CM的长为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)设点P坐标,表示出△PCD的面积,列出二次函数关系式,求出△PCD面积最大时的点P坐标,作PG⊥CD,PG即为PQ+![]() CQ;
CQ;
(2)等腰三角形分类讨论,分别以C、N和M为等腰顶点分别讨论,求出此时的点M坐标,获得CM线段长.
解:(1)当y=0时,![]() ,
,
解得:x1=﹣3,x2=4,
∴A(﹣3,0),B(4,0),
∵x=0时,y=4,
∴C (0,4),
设OD=m,则AD=m+3,
在Rt△AOC中,有AC2=AO2+OC2,
∴(m+3)2=32+42,
解得:m1=2,m=2﹣8
∴D(2,0),
如图1,设点P(m,n),
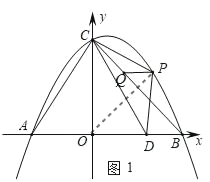
S△PCD=S△PCO+S△POD﹣S△COD
=![]()
=![]()
=![]()
=![]() ;
;
∵a=﹣![]() <0,则面积有最大值,
<0,则面积有最大值,
∴m=![]() 时,有最大值,
时,有最大值,
∴P(![]() ,
,![]() );
);
如图2,过点D作DH⊥CB,△DHB为等腰直角三角形,则DB=2,
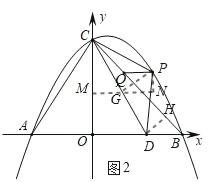
∴DH=BH=![]() ,
,
∵BC=![]() ,
,
∴CH=![]() ,
,
∴tan∠DCH=![]() .
.
过点P作PG⊥CD交BC于Q,则PG=PQ+![]() CQ,
CQ,
∴CD直线解析式为:y=﹣2x+4;
设G(m,﹣2m+4),
作GM⊥CO,PN⊥GM,垂足分别为M、N,可知△CMG∽△PGN,
∴![]() ,
,
∴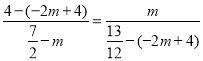 ,
,
解得:![]() ,
,
∵△CDO∽△GPN,
∴![]() ,
,
∴GP=![]() ,
,
∴PQ+![]() CQ的最小值为
CQ的最小值为![]() ;
;
(2)如图3,过点M1作M1H⊥AB,
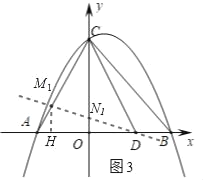
设直线L解析式为y=kx+b,
将(2,0)代入得:b=﹣2k,
∴y=kx﹣2k
①当CM1=CN1
∴ON1=﹣2k,CN1=4+2k,AM1=1﹣2k
∵△AM1H∽△AOC
∴![]() ,
,
∴![]() ,
,
∴AH=![]() (1﹣2k),M1H=
(1﹣2k),M1H=![]() ,
,
∴M1(![]() ,
,![]() ),
),
代入y=kx﹣2k得
![]() =k(
=k(![]() )﹣2k
)﹣2k
解得k1=﹣2,k2=![]() ,
,
∴CM=4+2k=![]() ;
;
②当CN2=MN2时,如图4
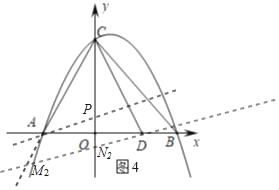
过A作AP∥BD,设AP直线解析式为y=kx+b,
将点A代入,﹣3k+b=0,
∴b=3k,
∴AP=![]() =
=![]() ,
,
∴CO=![]() +3k=4
+3k=4
∴k=![]() ,
,
∴DM直线解析式为:![]() ,
,
联立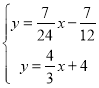 ,解得
,解得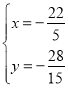
∴CM=![]() ;
;
③当M3C=M3N3时,如图5:
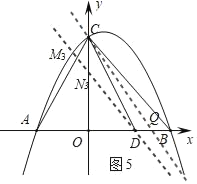
在x正半轴上取点Q(3,0),
∴CQ解析式为![]() ,
,
过点D作DM3∥CQ,
∴DM3的解析式为![]() ,
,
联立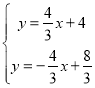 ,
,
解得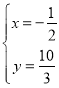 ,
,
∴M3(![]() ,
,![]() ),
),
∴CM3=![]() ;
;
综上所述:CM的长为:![]() 或
或![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案