题目内容
【题目】已知点 C、D是线段AB上两点（不与端点A、B重合），点A、B、C、D四点组成的所有线段的长度都是正整数，且总和为29，则线段AB的长度为__________________ .
【答案】8或9
【解析】
根据题意画出图形，可得图中共有线段6条，分别为AC、CD、DB，AD、BC、AB，然后根据所有线段的和为29可得关于AB、CD的等式，继而根据所有线段的长都是正整数以及AB>CD利用二元一次方程的解的概念进行求解即可.
如图，图中共有线段6条，分别为AC、CD、DB，AD、BC、AB，
由题意得：AC+CD+DB+AD+BC+AB=29，
∵AC+CD+DB=AB，AD=AC+CD，BC=CD+DB，
∴3AB+CD=29，
又∵所有线段的长度都是正整数，AB>CD ，
∴AB=8，CD=5或AB=9，CD=2，
即AB的长度为8或9，
故答案为：8或9.
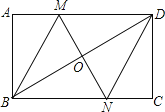
励耘书业暑假衔接宁波出版社系列答案【题目】如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连接BM、DN．
求证：四边形BMDN是菱形；
若
，
，求菱形BMDN的面积和对角线MN的长．
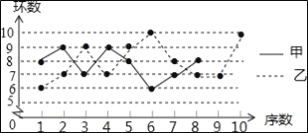
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹，成绩如表：
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且S乙2=1.8，根据上述信息完成下列问题：
（1）将甲运动员的折线统计图补充完整；
（2）乙运动员射击训练成绩的众数是_____，中位数是______．
（3）求甲运动员射击成绩的平均数和方差，并判断甲、乙两人本次射击成绩的稳定性．
【题目】有20筐橘子，以每筐20千克为标准，超过或不足的部分分别用正数或负数来表示，记录如下：
与标准重量的差(单位：千克) | －2 | －1.5 | －1 | 0 | 1 | 1.5 |
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)求最重的一筐比最轻的一筐重多少？
(2)求20筐橘子的总重量是多少千克？
