题目内容
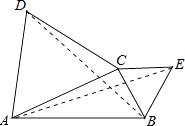
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q. 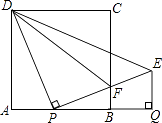
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.
【答案】
(1)解:根据题意得:PD=PE,∠DPE=90°,
∴∠APD+∠QPE=90°,
∵四边形ABCD是正方形,
∴∠A=90°,
∴∠ADP+∠APD=90°,
∴∠ADP=∠QPE,
∵EQ⊥AB,
∴∠A=∠Q=90°,
在△ADP和△QPE中,
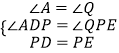 ,
,
∴△ADP≌△QPE(AAS),
∴PQ=AD=1
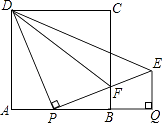
(2)解:∵△PFD∽△BFP,
∴ ![]() ,
,
∵∠ADP=∠EPB,∠CBP=∠A,
∴△DAP∽△PBF,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴PA=PB,
∴PA= ![]() AB=
AB= ![]()
∴当PA= ![]() ,即点P是AB的中点时,△PFD∽△BFP
,即点P是AB的中点时,△PFD∽△BFP
【解析】(1)由题意得:PD=PE,∠DPE=90°,又由正方形ABCD的边长为1,易证得△ADP≌△QPE,然后由全等三角形的性质,求得线段PQ的长;(2)易证得△DAP∽△PBF,又由△PFD∽△BFP,根据相似三角形的对应边成比例,可得证得PA=PB,则可求得答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目