题目内容
【题目】如图:在△ABC中,∠ABC=90°,AB=BC=8cm,动点P从点A出发,以2cm/s的速度沿射线AB运动,同时动点Q从点C出发,以2cm/s的速度沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t秒,△PCQ的面积为S cm2.
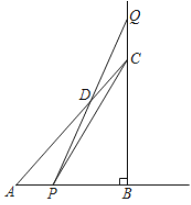
(1)直接写出AC的长:AC= cm;
(2)求出S关于t的函数关系式,并求出当点P运动几秒时,S△PCQ=S△ABC
【答案】(1)8![]() (2)2+2
(2)2+2![]()
【解析】
(1)在Rt△ABC中,利用勾股定理可求出AC的长;
(2)利用三角形的面积公式可找出S关于t的函数关系式,分0<t≤4和t>4两种情况,找出关于t的一元二次方程,解之取合适的值即可得出结论.
(1)在Rt△ABC中,∠ABC=90°,AB=BC=8cm,
∴AC=![]() =8
=8 ![]() cm.
cm.
故答案为:8![]() ;
;
(2)∵AP=CQ=2t,AB=8,
∴BP=|82t|,
∴S=![]() CQBP=t|82t|,
CQBP=t|82t|,
即S=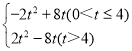 .
.
当0<t≤4时,2t2+8t=![]() AB×BC=
AB×BC=![]() ×8×8,
×8×8,
整理,得:t24t+16=0,
∵△=(4)24×1×16=48<0,
∴该方程无解;
当t>4时,2t28t=![]() ×8×8,
×8×8,
整理,得:t24t16=0,
解得:t1=22![]() (不合题意,舍去),t2=2+2
(不合题意,舍去),t2=2+2![]() .
.
∴当点P运动(2+2![]() )秒时,S△PCQ=S△ABC.
)秒时,S△PCQ=S△ABC.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目