题目内容
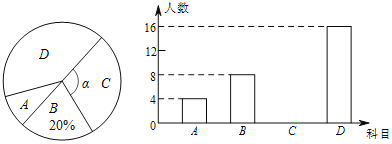
【题目】为提升学生的艺术素养，学习计划开设四门艺术选修课：A书法；B绘画；C乐器；D舞蹈，为了解学生对四门功课的喜欢情况，在全校范围内随机抽取若干名学生进行问卷调查（每个被调查的学生必须选择而且只能选择其中一门），将数据进行整理，并绘制成如下两幅不完整的统计图，请结合图中所给信息解答下列问题：
（1）本次调查的学生共有 人，扇形统计图中∠α的度数是 ；
（2）请把条形统计图补充完整；
（3）如果该校共有2500名学生，请你估计该校D类学生约有多少人？
【答案】（1）40，108°；（2）见解析；（3）该校2500名学生中D类的约有1000人
【解析】
（1）从两个统计图可得，“B组”的有8人，占调查人数的20%，可求出班级人数；样本中，“D组”占
，因此圆心角占360°的，可求出度数；
（2）求出“C组”人数，即可补全条形统计图：
（3）样本估计总体，样本中，“D组”占，估计总体500人的，是“D组”人数．
解：（1）8÷20%＝40（人），C组人数为40﹣4﹣8﹣16＝12（人），360°×
＝108°，
故答案为：40，108°，
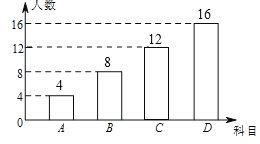
（2）补全条形统计图如图所示：
（3）2500×＝1000（人）．
答：该校2500名学生中D类的约有1000人．
【题目】为了调查A、B两个区的初三学生体育测试成绩，从两个区各随机抽取了1000名学生的成绩（满分：40分，个人成绩四舍五入向上取整数）
A区抽样学生体育测试成绩的平均分、中位数、众数如下：
平均分 | 中位数 | 众数 |
37 | 36 | 37 |
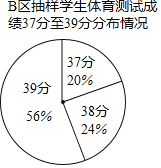
B区抽样学生体育测试成绩的分布如下：
成绩 | 28≤x＜31 | 31≤x＜34 | 34≤x＜37 | 37≤x＜40 | 40（满分） |
人数 | 60 | 80 | 140 | m | 220 |
请根据以上信息回答下列问题
（1）m＝ ；
（2）在两区抽样的学生中，体育测试成绩为37分的学生，在 （填“A”或“B”）区被抽样学生中排名更靠前，理由是 ；
（3）如果B区有10000名学生参加此次体育测试，估计成绩不低于34分的人数．
