题目内容
【题目】正方形 ABCD 中,AB=3cm,动点 M 自A 点出发沿 AB 方向以每秒 1cm 的速度运动,同时点 N 自D 点出发沿折线 DC→CB 以每秒 2cm 的速度运动,到达 B 点时运动同时停止,设△AMN 的面积为 y(cm2),运动时间为 x(秒),则下列图象中能大致反映 y 与 x 之间函数关系的是( )

A.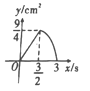 B.
B.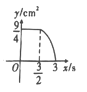 C.
C.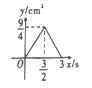 D.
D.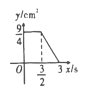
【答案】A
【解析】
分两部分计算y的关系式:①当点N在CD上时,易得S△AMN的关系式,S△AMN的面积关系式为一个一次函数;②当点N在CB上时,底边AM不变,表示出S△AMN的关系式,S△AMN的面积关系式为一个开口向下的二次函数.
∵点N自D点出发沿折线DCCB以每秒2cm的速度运动,到达B点时运动同时停止,
∴N到C的时间为:t=3÷2=1.5,
分两部分:
①当0x1.5时,如图1,此时N在DC上,
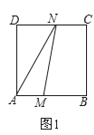
S△AMN=y=![]() AM×AD=
AM×AD=![]() x×3=
x×3=![]() x,S△AMN的面积关系式为一个一次函数
x,S△AMN的面积关系式为一个一次函数
②当1.5<x3时,如图2,此时N在BC上,
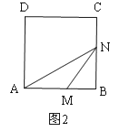
∴DC+CN=2x,
∴BN=62x,
∴S△AMN=y=![]() AM×BN=
AM×BN=![]() x(62x)=x2+3x,S△AMN的面积关系式为一个开口向下的二次函数.
x(62x)=x2+3x,S△AMN的面积关系式为一个开口向下的二次函数.
故选A.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目