题目内容
【题目】毕达哥拉斯学派对“数”与“形”的巧妙结合作了如下研究：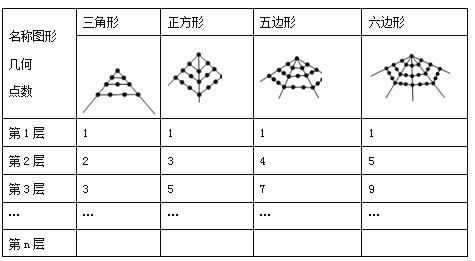
（1）六边形第5层的几何点数是 ；第n层的几何点数是 ．
（2）在第 层时，六边形的几何点数是三角形的几何点数的3.5倍．
【答案】17；4n-3；6
【解析】解：（1）∵六边形第1层几何点数：1=4×1﹣3；
六边形第2层几何点数：5=4×2﹣3；
六边形第3层几何点数：9=4×3﹣3；
∴六边形第5层几何点数为：4×5﹣3=17，
六边形第n层几何点数为：4n﹣3；
（2）∵三角形第一层点数为1，第二层点数为2，第三层点数为3，
∴三角形第n层的几何点数为n；
由六边形的几何点数是三角形的几何点数的3.5倍，得
4n﹣3=3.5n，解得n=6；
则在第6层时，六边形的几何点数是三角形的几何点数的3.5倍．
所以答案是：（1）17，4n﹣3；（2）6．
【考点精析】认真审题，首先需要了解解一元一次方程的步骤(先去分母再括号，移项变号要记牢．同类各项去合并，系数化“1”还没好．求得未知须检验，回代值等才算了)．
练习册系列答案
相关题目
