题目内容
【题目】如图,在等腰直角△ABC中, ![]() 点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且
点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且![]() .
.
(1)判断![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)若BE=12,CF=5,求△![]() 的面积.
的面积.

【答案】(1)DF=DE;(2)△DEF的面积是![]()
【解析】试题分析:(1)连接AD,首先利用等腰三角形的性质得到AD⊥BC,AD=CD=BD,从而得到∠CDF=∠ADE,然后利用ASA证得DCF≌△ADE后即可证得DF=DE;
(2)由(1)知:AE=CF,AF=BC,DE=DF,即△EDF为等腰直角三角形,在Rt△AEF中,运用勾股定理可将EF的值求出,进而可求出DE、DF的值,代入S△EDF=![]() DE2进行求解.
DE2进行求解.
试题解析:(1)DF=DE,理由如下:
如图,连接AD,
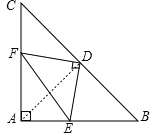
∵AB=AC,D为BC的中点,
∴AD⊥BC,AD=CD=BD,
∵DE⊥DF,
∴∠CDF+∠ADF=∠EDA+∠ADF,
即∠CDF=∠ADE,
在△DCF和△DAE中,
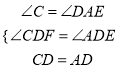 ,
,
∴△DCF≌△DAE(ASA),
∴DF=DE;
(2)由(1)知:AE=CF=5,同理AF=BE=12.
∵∠EAF=90°,
∴EF2=AE2+AF2=52+122=169.
∴EF=13,
又∵由(1)知:△AED≌△CFD,
∴DE=DF,
∴△DEF为等腰直角三角形,DE2+DF2=EF2=169,
∴DE=DF=![]() ,
,
∴S△DEF=![]() ×(
×(![]() )2=
)2=![]() .
.

练习册系列答案
相关题目