题目内容
【题目】如图1,四边形ABCD中,BD⊥AD,E为BD上一点,AE=BC,CE⊥BD,CE=ED

(1)已知AB=10,AD=6,求CD;
(2)如图2,F为AD上一点,AF=DE,连接BF,交BF交AE于G,过G作GH⊥AB于H,∠BGH=75°.求证:BF=2![]() GH+
GH+![]() EG.
EG.
【答案】(1)2![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)由勾股定理得出BD=![]() =8,由HL证得Rt△ADE≌Rt△BEC,得出BE=AD,则CE=ED=BD﹣BE=BD﹣AD=2,由等腰直角三角形的性质即可得出结果;
=8,由HL证得Rt△ADE≌Rt△BEC,得出BE=AD,则CE=ED=BD﹣BE=BD﹣AD=2,由等腰直角三角形的性质即可得出结果;
(2)连接CF,易证AF=CE,AD∥CE,得出四边形AECF是平行四边形,则AE=CF,AE∥CF,得出∠CFD=∠EAD,∠CFB=∠AGF,由Rt△ADE≌Rt△BEC,得出∠CBE=∠EAD,推出∠CBE=∠CFD,证得△BCF是等腰直角三角形,则BF=![]() BC=
BC=![]() CF=
CF=![]() AE,∠FBC=∠BFC=45°,推出∠AGF=45°,∠AGH=60°,∠GAH=30°,则AG=2GH,得出BF=
AE,∠FBC=∠BFC=45°,推出∠AGF=45°,∠AGH=60°,∠GAH=30°,则AG=2GH,得出BF=![]() AE=
AE=![]() (AG+EG),即可得出结论.
(AG+EG),即可得出结论.
(1)解:∵BD⊥AD,
∴BD=![]() =
=![]() =8,
=8,
∵CE⊥BD,
∴∠CEB=∠EDA=90°,
在Rt△ADE和Rt△BEC中,![]() ,
,
∴Rt△ADE≌Rt△BEC(HL),
∴BE=AD,
∴CE=ED=BD﹣BE=BD﹣AD=8﹣6=2,
∴CD![]() =CE=2
=CE=2![]() ;
;
(2)解:连接CF,如图2所示:
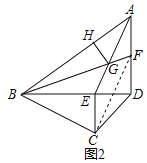
∵AF=DE,DE=CE,
∴AF=CE,
∵BD⊥AD,CE⊥BD,
∴AD∥CE,
∴四边形AECF是平行四边形,
∴AE=CF,AE∥CF,
∴∠CFD=∠EAD,∠CFB=∠AGF,
由(1)得:Rt△ADE≌Rt△BEC,
∴∠CBE=∠EAD,
∴∠CBE=∠CFD,
∵∠FBD+∠BFC+∠CFD=90°,
∴∠FBD+∠BFC+∠CBE=90°,
∴∠BCF=90°,
∵AE=BC,
∴BC=CF,
∴△BCF是等腰直角三角形,
∴BF=![]() BC=
BC=![]() CF=
CF=![]() AE,∠FBC=∠BFC=45°,
AE,∠FBC=∠BFC=45°,
∴∠AGF=45°,
∵∠BGH=75°,
∴∠AGH=180°﹣45°﹣75°=60°,
∵GH⊥AB,
∴∠GAH=30°,
∴AG=2GH,
∴BF=![]() AE=
AE=![]() (AG+EG),
(AG+EG),
∴BF=2![]() GH+
GH+![]() EG.
EG.