题目内容
【题目】平面直角坐标系中,已知点A(2,2),B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )

A.3B.4C.5D.6
【答案】C
【解析】
由点A、B的坐标可得到![]() ,然后分类讨论:若AC=AB;若BC=AB;若CA=CB,确定C点的个数.
,然后分类讨论:若AC=AB;若BC=AB;若CA=CB,确定C点的个数.
∵点A、B的坐标分别为(2,2)、B(4,0).
∴![]() ,
,
①若AC=AB,以A为圆心,AB为半径画弧与坐标轴有3个交点(含B点),即(0,0)、(4,0)、(0,4),
∵点(0,4)与直线AB共线,
∴满足△ABC是等腰三角形的C点有1个;
②若BC=AB,以B为圆心,BA为半径画弧与坐标轴有2个交点(A点除外),即满足△ABC是等腰三角形的C点有2个;
③若CA=CB,作AB的垂直平分线与坐标轴有两个交点,即满足△ABC是等腰三角形的C点有2个;
综上所述:点C在坐标轴上,△ABC是等腰三角形,符合条件的点C共有5个.
故选:C.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
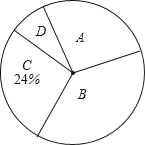
【题目】某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
(1)表中的a= ,b= ;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?