ЬтФПФкШн
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬ2x2+4x+k-1=0гаЪЕЪ§ИљЃЌkЮЊе§ећЪ§.
ЃЈ1ЃЉЧѓkЕФжЕЃЛ
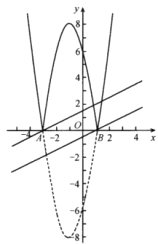
ЃЈ2ЃЉЕБДЫЗНГЬгаСНИіЗЧСуЕФећЪ§ИљЪБЃЌНЋЙигкxЕФЖўДЮКЏЪ§y=2x2+4x+k-1ЕФЭМЯѓЯђЯТЦНвЦ8ИіЕЅЮЛЃЌЧѓЦНвЦКѓЕФЭМЯѓЕФНтЮіЪНЃЛ
(3) дкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋЦНвЦКѓЕФЖўДЮКЏЪ§ЕФЭМЯѓдкxжсЯТЗНЕФВПЗжбиxжсЗелЃЌЭМЯѓЕФЦфгрВПЗжБЃГжВЛБфЃЌЕУЕНвЛИіаТЕФЭМЯѓ.ЧыФуНсКЯетИіаТЕФЭМЯёЛиД№ЃКЕБжБЯпy=0.5x+b (b<k)гыДЫЭМЯѓгаСНИіЙЋЙВЕуЪБЃЌbЕФШЁжЕЗЖЮЇ.
ЁОД№АИЁПЃЈ1ЃЉkЃН1ЃЌ2ЃЌ3ЃЛ
ЃЈ2ЃЉЭМЯѓЕФНтЮіЪНЮЊyЃН2x2ЃЋ4xЃ6ЃЛ
ЃЈ3ЃЉb(bЃМ3)ЕФШЁжЕЗЖЮЇЮЊ-0.5<b<1.5ЃЎ
ЁОНтЮіЁПНтЃК(1)гЩЬтвтЕУЃЌІЄЃН16Ѓ8(kЃ1)Ён0ЃЎЁрkЁм3ЃЎЁпkЮЊе§ећЪ§ЃЌЁрkЃН1ЃЌ2ЃЌ3ЃЎ
(2)ЕБkЃН1ЪБЃЌЗНГЬ2x2ЃЋ4xЃЋkЃ1ЃН0гавЛИіИљЮЊСуЃЛ
ЕБkЃН2ЪБЃЌЗНГЬ2x2ЃЋ4xЃЋkЃ1ЃН0ЮоећЪ§ИљЃЛ
ЕБkЃН3ЪБЃЌЗНГЬ2x2ЃЋ4xЃЋkЃ1ЃН0гаСНИіЗЧСуЕФећЪ§ИљЃЎ
злЩЯЫљЪіЃЌkЃН1КЭkЃН2ВЛКЯЬтвтЃЌЩсШЅЃЛkЃН3ЗћКЯЬтвтЃЎ
ЕБkЃН3ЪБЃЌЖўДЮКЏЪ§ЮЊyЃН2x2ЃЋ4xЃЋ2ЃЌАбЫќЕФЭМЯѓЯђЯТЦНвЦ8ИіЕЅЮЛГЄЖШЕУЕНЕФЭМЯѓЕФНтЮіЪНЮЊyЃН2x2ЃЋ4xЃ6ЃЎ
(3)ЩшЖўДЮКЏЪ§yЃН2x2ЃЋ4xЃ6ЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌдђA(Ѓ3ЃЌ0)ЃЌB(1ЃЌ0)ЃЎ
вРЬтвтЗелКѓЕФЭМЯѓШчЭМЫљЪОЃЎ
ЕБжБЯпy=0.5x+bОЙ§AЕуЪБЃЌПЩЕУb=1.5ЃЛ
ЕБжБЯпy=0.5x+bОЙ§BЕуЪБЃЌПЩЕУ-0.5ЃЎ
гЩЭМЯѓПЩжЊЃЌЗћКЯЬтвтЕФb(bЃМ3)ЕФШЁжЕЗЖЮЇЮЊ-0.5<b<1.5ЃЎ