题目内容
【题目】如图所示,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则EF长为cm. 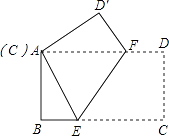
【答案】![]()
【解析】解:如图所示,连接AC、CF, 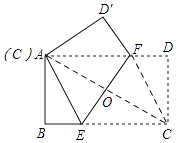
由折叠可知,EF⊥AC,
又∵AF∥CE,
∴∠FAO=∠ECO,
在△AOF与△COE中,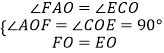 ,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴四边形AECF是平行四边形,
又∵EF垂直平分AC,
∴AE=AF,
∴四边形AECF为菱形,(有一组邻边相等的平行四边形是菱形)
设AE=EC=xcm,则BE=(8﹣x)cm,
在Rt△ABC中,由勾股定理得:AC=10cm,
在Rt△ABE中,由勾股定理得:AB2+BE2=AE2 ,
即62+(8﹣x)2=x2 ,
解得x= ![]() ,
,
根据菱形计算面积的公式,得
EC×BA= ![]() ×EF×AC,
×EF×AC,
即 ![]() ×6=
×6= ![]() ×EF×10,
×EF×10,
解得EF= ![]() cm.
cm.
故答案为: ![]() .
.
连接AC、CF,利用折叠的性质证明四边形AECF为菱形,设AE=EC=x,在Rt△ABC中,由勾股定理求AC,在Rt△ABE中,由勾股定理求x,利用菱形计算面积的两种方法,建立等式求EF即可.

练习册系列答案
相关题目