题目内容
【题目】某单位计划购买电脑若干台,经了解同一型号市场预售价均为每台5000元.现有两商场优惠促销,甲商场:购买不超过2台按原价销售,超过2台的部分每台打7折;乙商场:每台均打8折.
(1)若学校购买5台,哪家商场较优惠?购买7台呢?
(2)买多少台时两商场所需费用一样多?
(3)你知道学校怎样选购更省钱?
【答案】(1)购买5台,乙商场更优惠;购买7台,甲商场更优惠;(2)6;(3)答案见解析.
【解析】试题分析:(1)根据甲乙两个商场的促销方案分别计算出学校购买5台和7台电脑所需的费用,比较即可;(2)设购买![]() 台时,两商场所需要费用一样多,根据费用一样多列出方程,解方程即可;(3)在(2)的基础上,比较即可.
台时,两商场所需要费用一样多,根据费用一样多列出方程,解方程即可;(3)在(2)的基础上,比较即可.
试题解析:
(1)购买5台,甲商场:![]()
乙商场: ![]() ,
,![]() ,
, ![]() 乙商场更优惠.
乙商场更优惠.
购买7台,甲商场:![]() ,乙商场:
,乙商场: ![]() .
.
![]() 27500元<28000元,
27500元<28000元, ![]() 甲商场更优惠.
甲商场更优惠.
(2)设购买![]() 台时,两商场所需要费用一样多,根据题意得
台时,两商场所需要费用一样多,根据题意得
![]() ,解得:
,解得: ![]() .
.
答:当购买![]() 台时,两商场所需要费用一样多.
台时,两商场所需要费用一样多.
(3)当购买台数小于6时,在乙商场更省钱;
当购买台数等于6时,两商场一样省钱;
当购买台数大于6时,在甲商场更省钱.
【题型】解答题
【结束】
26
【题目】已知∠AOB=90°,![]() 是锐角,ON平分
是锐角,ON平分![]() ,OM平分∠AOB.
,OM平分∠AOB.
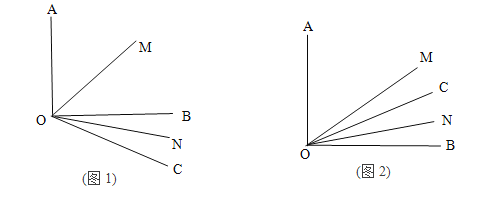
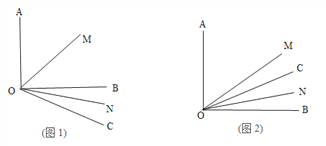
(1)如图1若![]() =30°,求
=30°,求![]() 的度数?
的度数?
(2)若射线OC绕着点O运动到∠AOB的内部(如图2),在(1)的条件下求![]() 的度数;
的度数;
(3)若∠AOB=![]() (90°≤
(90°≤![]() <180°),
<180°),![]() =
= ![]() (0°<
(0°<![]() <90°),请用含有
<90°),请用含有![]() 的式子直接表示上述两种情况
的式子直接表示上述两种情况![]() 的度数.
的度数.
【答案】(1)60°;(2)30°;(3)①∠MON=![]() (
(![]() +
+![]() ),;②∠MON=
),;②∠MON=![]() (
(![]() -
-![]() ).
).
【解析】试题分析:(1)由于∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,所以可以求得∠MOB和∠NOB的度数,进而求得∠MON的度数;(2)类比(1)的方法求解即可;(3)结合(1)(2)题的计算方法求解即可.
试题解析:
(1)∵OM平分∠AOB,ON平分∠BOC,
∴∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOC.
∠BOC.
∵∠AOB=90°,∠BOC=30°,
∴∠BOM=![]() ×90°=45°,∠BON=
×90°=45°,∠BON=![]() ×30°=15°,
×30°=15°,
∴∠MON=∠BOM+∠BON=45°+15°=60°.
(2)由(1)可知:∠BOM=45°,∠BON=15°,
∴∠MON=∠BOM-∠BON=45°-15°=30°.
(3)①∠MON=![]() (
(![]() +
+![]() ),②∠MON=
),②∠MON=![]() (
(![]() -
-![]() ).
).