题目内容
(本题满分12分)如图,抛物线y=a(x+1)(x-5)与x轴的交点为M、N.直线y=kx+b
与x轴交于P(-2,0),与y轴交于C.若A、B两点在直线y=kx+b上,且AO=BO= ,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.
,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.
(1)OH的长度等于___________;k=___________,b=____________;
(2)是否存在实数a,使得抛物线y=a(x+1)(x-5)上有一点E,满足以D、N、E为顶
 点的三角形与△AOB相似?若不存在,说明理由;若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由);并进一步探索对符合条件的每一个E点,直线NE与直线AB的交点G是否总满足PB·PG<
点的三角形与△AOB相似?若不存在,说明理由;若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由);并进一步探索对符合条件的每一个E点,直线NE与直线AB的交点G是否总满足PB·PG< ,写出探索过程.
,写出探索过程.
见解析
【解析】(1)OH=1;k=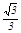 ,b=
,b=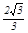 ; (各1分)
; (各1分)
(2)设存在实数a,是抛物线y=a (x+1)(x-5)上有一点E,满足以D、N、E为顶点的三角形与等腰直角△AOB相似
∴以D、N、E为顶点的三角形为等腰直角三角形,且这样的三角形最多只有两类,一类是以DN为直角边的等腰直角三角形,另一类是以DN为斜边的等腰直角三角形.
①若DN为等腰直角三角形的直角边,则ED⊥DN.
由抛物线y=a(x+1)(x-5)得:M(-1,0),N(5,0)
∴D(2,0),∴ED=DN=3,∴E的坐标是(2,3).
把E(2,3)代入抛物线解析式,得a=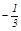
∴抛物线解析式为y=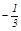 (x+1)(x-5)
(x+1)(x-5)
即y=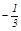 x2+
x2+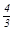 x+
x+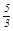 (2分)
(2分)
②若DN为等腰直角三角形的斜边,则DE⊥EN,DE=EN.
∴E的坐标为(3.5,1.5)
把E(3.5,1.5)代入抛物线解析式,得a=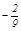 .
.
∴抛物线解析式为y=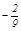 (x+1)(x-5),即y=
(x+1)(x-5),即y=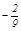 x2+
x2+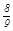 x+
x+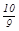 (2分)
(2分)
当a=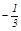 时,在抛物线y=
时,在抛物线y=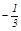 x2+
x2+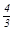 x+
x+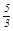 上存在一点E(2,3)满足条件,如果此抛物线上还有满足条件的E点,不妨设为E’点,那么只有可能△DE’N是以DN为斜边的等腰直角三角形,由此得E’(3.5,1.5).显然E’不在抛物线y=
上存在一点E(2,3)满足条件,如果此抛物线上还有满足条件的E点,不妨设为E’点,那么只有可能△DE’N是以DN为斜边的等腰直角三角形,由此得E’(3.5,1.5).显然E’不在抛物线y=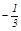 x2+
x2+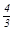 x+
x+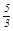 上,因此抛物线y=
上,因此抛物线y=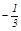 x2+
x2+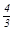 x+
x+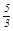 上没有符合条件的其他的E点. (1分)
上没有符合条件的其他的E点. (1分)
当a=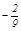 时,同理可得抛物线y=
时,同理可得抛物线y=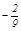 x2+
x2+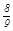 x+
x+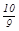 上没有符合条件的其他的E点.
上没有符合条件的其他的E点.
(1分)
当E的坐标为(2,3),对应的抛物线解析式为y=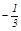 x2+
x2+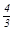 x+
x+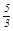 时.
时.
∵△EDN和△ABO都是等腰直角三角形,∴∠GNP=∠PBO=45°.
又∵∠NPG=∠BPO,∴△NPG∽△BPO.
∴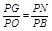 ,∴PB·PG=PO·PN=2×7=14,∴总满足PB·PG<
,∴PB·PG=PO·PN=2×7=14,∴总满足PB·PG<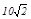 . (2分)
. (2分)
当E的坐标为(3.5,1.5),对应的抛物线解析式为y=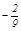 x2+
x2+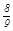 x+
x+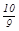 时,
时,
同理可证得:PB·PG=PO·PN=2×7=14,∴总满足PB·PG<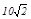 . (1分)
. (1分)

(本题满分12分)
如图, 的顶点A、B在二次函数
的顶点A、B在二次函数 的图像上,又点A、B[来分别在
的图像上,又点A、B[来分别在 轴和
轴和 轴上,
轴上, ∠ABO=
∠ABO= .
.

1.(1)求此二次函数的解析式;(4分)
2.
|
 作
作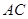 ∥
∥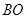 交上述函数图像于点
交上述函数图像于点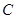 ,
,
点 在上述函数图像上,当
在上述函数图像上,当 与
与 相似时,求点
相似时,求点 的坐标.(8分)
的坐标.(8分)

 的长;
的长;
 与x轴交于A、C两点,与y轴交于B点,与直线
与x轴交于A、C两点,与y轴交于B点,与直线 交于A、D两点。
交于A、D两点。 落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?

 ,
, ,
, .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
 时,求线段
时,求线段 的长;
的长; 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.