题目内容
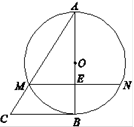
如图,⊙C经过原点且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.⊙C圆心C的坐标是 .


(- ,2).
,2).
 ,2).
,2).试题分析:连接AB,AM,则由∠AOB=90°,故AB是直径.
由∠BAM+∠OAM=∠BOM+∠OBM=180°-120°=60°,得∠BAO=60°.
又∵AO=4,∴
 .∴⊙C的半径为4,
.∴⊙C的半径为4, .
.过C作CE⊥OA于E,CF⊥OB于F,则
 .
.∴C点坐标为(-
 ,2).
,2).

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
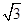 .
.
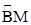 的长.
的长.
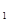 与⊙O
与⊙O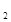 的半径分别是3、4,圆心距为1,则两圆的位置关系是( )
的半径分别是3、4,圆心距为1,则两圆的位置关系是( )
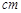 ,母线长为4
,母线长为4 线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
 B.
B. C.
C. D.
D.