题目内容
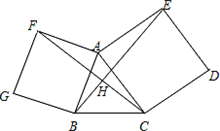
 17、如图,以锐角△ABC的边AB、AC向外作正方形APQB和正方形AEFC,连接PE,作AD⊥BC,垂足为D,延长DA交PE于点H.过P作PM⊥DM,垂足为M,过点E作EN⊥DM,垂足为N.
17、如图,以锐角△ABC的边AB、AC向外作正方形APQB和正方形AEFC,连接PE,作AD⊥BC,垂足为D,延长DA交PE于点H.过P作PM⊥DM,垂足为M,过点E作EN⊥DM,垂足为N.(1)不再增加线条或字母,在图中找出一对全等三角形,并给出证明;
(2)求证:PH=HE.
分析:(1)此题中,较明显的全等三角形是△BAD≌△APM,△DAC≌△NEA;以第一组全等三角形为例:由于四边形ABQP是正方形,可得两个条件:AP=AB,∠BAP=90°;由∠BAP=90°,易证得∠PAM=∠ABD,联立AP=AB和一组直角,即可得证,第二组全等三角形证法相同;
那么另一组全等三角形是:△PMH≌△ENH,思路:由上面的两组全等三角形得:PM=NE=AD;而∠PMH、∠ENH都是直角,且有一组对顶角相等,由AAS即可证得两个三角形全等.
(2)由(1)中得到的第三组全等三角形,即可得证.
那么另一组全等三角形是:△PMH≌△ENH,思路:由上面的两组全等三角形得:PM=NE=AD;而∠PMH、∠ENH都是直角,且有一组对顶角相等,由AAS即可证得两个三角形全等.
(2)由(1)中得到的第三组全等三角形,即可得证.
解答:解:(1)有三组:△BAD≌△APM,△DAC≌△NEA,△PMH≌△ENH;任选一组即可;
以△BAD≌△APM为例进行说明;
证明:∵四边形ABQP是正方形,
∴AB=AP,∠PAB=90°;
∴∠PAM=∠ABD=90°-∠BAD,
又∵∠PMA=∠ADB=90°,
∴△BAD≌△APM;
(△DAC≌△NEA证法同上,△PMH≌△ENH如(2).)
(2)由(1)的△BAD≌△APM,△DAC≌△NEA,得:PM=NE=AD;
∵∠PMH=∠ENH=90°,∠PHM=∠EHN,
∴△PMH≌△ENH,故PH=HE.
以△BAD≌△APM为例进行说明;
证明:∵四边形ABQP是正方形,
∴AB=AP,∠PAB=90°;
∴∠PAM=∠ABD=90°-∠BAD,
又∵∠PMA=∠ADB=90°,
∴△BAD≌△APM;
(△DAC≌△NEA证法同上,△PMH≌△ENH如(2).)
(2)由(1)的△BAD≌△APM,△DAC≌△NEA,得:PM=NE=AD;
∵∠PMH=∠ENH=90°,∠PHM=∠EHN,
∴△PMH≌△ENH,故PH=HE.
点评:此题主要考查了正方形的性质和全等三角形的判定,难度适中.

练习册系列答案
相关题目
 24、如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.
24、如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.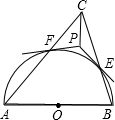 如图,以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F.过点E、F分别作⊙O的切线得交点P.求证:CP⊥AB.
如图,以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F.过点E、F分别作⊙O的切线得交点P.求证:CP⊥AB. 26、如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.
26、如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.