题目内容
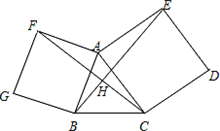
26、如图，以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF，连接BE、CF．（1）哪两个图形可以通过旋转而相互得到？请指出旋转中心和旋转角．
（2）试探索BE和CF的数量和位置关系？直接写出结果，不必说明理由．
分析：（1）观察△ABE和△AFC的位置关系，可确定旋转中心，旋转方向，旋转角；
（2）由旋转的性质可知，旋转前后的三角形全等，可知对应边相等，即BE=CF，利用互余关系可证BE⊥CF．
（2）由旋转的性质可知，旋转前后的三角形全等，可知对应边相等，即BE=CF，利用互余关系可证BE⊥CF．
解答：解：（1）△ABE和△AFC可以通过旋转而相互得到，旋转中心是A，旋转角为90°；
（2）BE=CF，BE⊥CF．
理由如下：
∵△ABE和△AFC可以通过旋转而相互得到，旋转中心是A，旋转角为90°，
∴BE=CF，BE⊥CF．
（2）BE=CF，BE⊥CF．
理由如下：
∵△ABE和△AFC可以通过旋转而相互得到，旋转中心是A，旋转角为90°，
∴BE=CF，BE⊥CF．
点评：本题考查了旋转的性质，正方形的性质及三角形全等的性质，关键是根据图形中两个三角形的位置关系解题．
练习册系列答案
名校课堂系列答案
相关题目
17、如图，以锐角△ABC的边AB、AC向外作正方形APQB和正方形AEFC，连接PE，作AD⊥BC，垂足为D，延长DA交PE于点H．过P作PM⊥DM，垂足为M，过点E作EN⊥DM，垂足为N．
24、如图，以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF，连接BE、CF．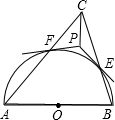
如图，以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F．过点E、F分别作⊙O的切线得交点P．求证：CP⊥AB．