题目内容
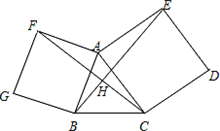
24、如图，以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF，连接BE、CF．（1）试探索BE和CF的关系？并说明理由．
（2）你能找到哪两个图形可以通过旋转而相互得到，并指出旋转中心和旋转角．
分析：要求两条线段的长度关系，把两条线段放到两个三角形中，利用三角形的全等求得两条线段相等．
解答：解：（1）BE和CF垂直且相等．
理由：先AB和CF的交点为O，如下图所示：
在正方形ABGF，
AF=AB，
∠FAB=90°，
又在正方形ACDE，
AE=AC，
∠EAC=90°，
∴∠FAB=∠EAC=90°，
∵∠FAC=∠FAB+∠BAC，
∠EAB=∠EAC+∠BAC，
∴∠FAC=∠EAB，
∴△FAC≌△EAB，
∴BE=CF，且∠AFC=∠ABE，
又∠AOF=∠BOH，
故在△AFO和△BHO中，有∠FAO=∠BHO=90°，
∴BE又垂直于CF；
（2）由（1）知，△FAC≌△BAE，
故△FAC和B△AE可以通过旋转而得到彼此，
其旋转中心为点A，旋转角为直角．
理由：先AB和CF的交点为O，如下图所示：
在正方形ABGF，
AF=AB，
∠FAB=90°，
又在正方形ACDE，
AE=AC，
∠EAC=90°，
∴∠FAB=∠EAC=90°，
∵∠FAC=∠FAB+∠BAC，
∠EAB=∠EAC+∠BAC，
∴∠FAC=∠EAB，
∴△FAC≌△EAB，
∴BE=CF，且∠AFC=∠ABE，
又∠AOF=∠BOH，
故在△AFO和△BHO中，有∠FAO=∠BHO=90°，
∴BE又垂直于CF；
（2）由（1）知，△FAC≌△BAE，
故△FAC和B△AE可以通过旋转而得到彼此，
其旋转中心为点A，旋转角为直角．
点评：本题考查了正方形和旋转的性质，及全等三角形的判定与性质，对各个基础知识点的熟练掌握是关键．
练习册系列答案
相关题目
17、如图，以锐角△ABC的边AB、AC向外作正方形APQB和正方形AEFC，连接PE，作AD⊥BC，垂足为D，延长DA交PE于点H．过P作PM⊥DM，垂足为M，过点E作EN⊥DM，垂足为N．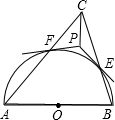
如图，以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F．过点E、F分别作⊙O的切线得交点P．求证：CP⊥AB．
26、如图，以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF，连接BE、CF．