��Ŀ����
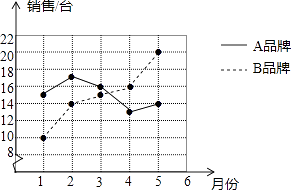
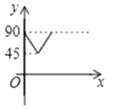
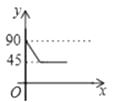
����Ŀ��ij��˾Ͷ��1200��Ԫ������һ���������������²�Ʒ�������г����У�����ÿ����Ʒ��Ҫ�ɱ�50Ԫ���ò�Ʒ�����г��õ���80Ԫ/���Ҳ��ó���160Ԫ/�����ò�Ʒ������y����������Ʒ�ۼ�x��Ԫ��֮��Ĺ�ϵ��ͼ��ʾ��
��1����y��x֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2����һ�깫˾��ӯ�����ǿ��������ӯ�����������Сʱ�IJ�Ʒ�ۼۣ�
��3���ڣ�2����ǰ���£����ڵ�һ��ӯ�������߿�����Сʱ����˾�ڶ�������ȷ����Ʒ�ۼۣ��ܷ�ʹǰ����ӯ���ܶ��790��Ԫ�����ܣ�����ڶ����Ʒ�ۼۣ������ܣ�˵�����ɣ�
���𰸡�
��1���⣺��y=kx+b����ͼ��ɵã� ![]() ��
��
��ã� 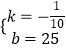 ��
��
����y=�� ![]() x+25��
x+25��
��x��ȡֵ��Χ��80��x��160��
��2���⣺��ù�˾��һ�����S��Ԫ����
S=��x��50����y��1200=��x��50������ ![]() x+25����1200
x+25����1200
=�� ![]() x2+30x��2450
x2+30x��2450
=�� ![]() ��x��150��2��200�ܩ�200��
��x��150��2��200�ܩ�200��
���Ե�һ�깫˾�ǿ����ҵ�������Сʱ�IJ�Ʒ�ۼ�Ϊ150Ԫ/����
��3���⣺��������з��̣�x��50������ ![]() x+25��+����200��=790��
x+25��+����200��=790��
��ã�x1=140��x2=160��
����x��ֵ����80��x��160�ڣ�
���Եڶ����ۼ���140Ԫ/����160/����
����������1�����ݺ���ͼ��õ���������꣬�������y��x֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ����2�����������г���ʽ���õ����κ����Ķ���ʽ�������������ֵ���õ���һ�깫˾�ǿ����ҵ�������Сʱ�IJ�Ʒ�ۼۣ���3�����ݺ�������ֵ�г����̣�����ڶ����Ʒ�ۼ�.