题目内容
【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=![]() ,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是_____.
,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是_____.

【答案】![]()
【解析】
作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值;证出△ONN′为等边三角形,△OMM′为等边三角形,得出∠N′OM′=90°,由勾股定理求出M′N′即可.
解:作M关于OB的对称点M′,作N关于OA的对称点N′,如图所示:
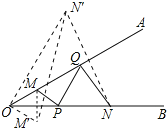
连接M′N′,即为MP+PQ+QN的最小值.
根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,
∴△ONN′为等边三角形,△OMM′为等边三角形,
∴∠N′OM′=90°,OM′=OM=![]() ,ON′=ON=6,
,ON′=ON=6,
∴在Rt△M′ON′中,
M′N′=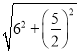 =
=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】九(2)班组织了一次朗读比赛,甲、乙两队各10人的比赛成绩(10分制)如下表(单位:分):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算乙队成绩的平均数和方差;
(3)已知甲队成绩的方差是1.4分2 , 则成绩较为整齐的是队.