题目内容
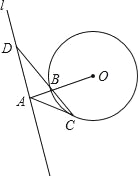
【题目】如图,在△MNQ中,MN=11,NQ=![]() ,
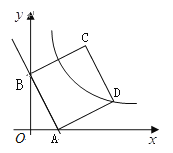
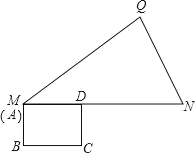
,![]() ,矩形ABCD,BC=4,CD=3,点A与M重合,AD与MN重合.矩形ABCD沿着MQ方向平移,且平移速度为每秒5个单位,当点A与Q重合时停止运动.
,矩形ABCD,BC=4,CD=3,点A与M重合,AD与MN重合.矩形ABCD沿着MQ方向平移,且平移速度为每秒5个单位,当点A与Q重合时停止运动.
(1)MQ的长度是 ;
(2)运动 秒,BC与MN重合;
(3)设矩形ABCD与△MNQ重叠部分的面积为S,运动时间为t,求出S与t之间的函数关系式.
【答案】(1) 10 ;(2) 1 ;(3)S=12t;S=12;S=﹣8.25t+22.5;S=﹣![]() t+35.
t+35.
【解析】试题分析:(1)过Q作QH⊥MN于H,根据![]()
![]() 求出NH=3,求出MH,根据勾股定理求出QH,即可求出答案;
求出NH=3,求出MH,根据勾股定理求出QH,即可求出答案;
(2)连接BD,解直角三角形求出QM∥BD,当BC和MN重合时,B正好到D点,求出BD的长即可;
(3)分为四种情况:①当BC运动到MN上时;②当点D运动到QN上时;③当C运动到QN上时;④当C运动到△QMN的外部,即![]() <t≤2时.
<t≤2时.
解:(1)如图1,过Q作QH⊥MN于H,
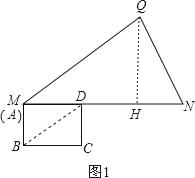
∵QN=3![]() ,cosN=
,cosN=![]() =
=![]() ,
,
∴NH=3,
∴MH=11﹣3=8,
在Rt△NHQ中,由勾股定理得:QH=![]() =6,
=6,
在Rt△QMH中,由勾股定理得:MQ=![]() =10,
=10,
故答案为:10.
(2)连接BD,如图1,
∵tan∠ABD=![]() =
=![]() ,tan∠QMN=
,tan∠QMN=![]() =
=![]() =
=![]() ,
,
∴QM∥BD,
当BC和MN重合时,B正好到D点,由勾股定理得:BD=5,
5÷5=1,
即运动1秒时,BC和MN重合,
故答案为:1.
(3)分为四种情况:
①当BC运动到MN上时,此时0<t≤1,如图2,
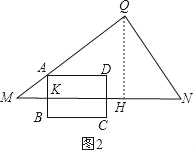
∵sinM=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AK=3t,
∵AD=4,
∴S=43t=12t;
②当D到QN上时,此时1<t≤![]() ,如图3,
,如图3,
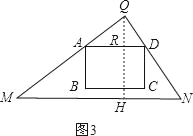
∵△QAD∽△QMN,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴QR=![]() ,
,
∵AD∥MN,
∴△QAR∽△QMH,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴t=![]() ,
,
即此时1<t≤![]() ,
,
S=3×4=12;
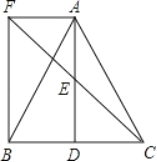
③当C到QN上时,此时![]() <t≤
<t≤![]() ,如图4,
,如图4,
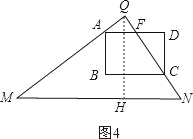
∵AD∥MN,
∴∠AFQ=∠N=∠DFC,
∵∠D=∠QHN=90°,
∴△DFC∽△HNQ,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴DF=1.5,
AF=4﹣1.5=2.5,
∵AD∥MN,
∴△QAF∽△QMN,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴t=![]() ,
,
即当C到QN上时,t=![]() ,
,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AF=11﹣5.5t,
S=![]() (AF+BC)×CD
(AF+BC)×CD
=![]() (11﹣5.5t+4)3,
(11﹣5.5t+4)3,
S=﹣8.25t+22.5;
④当![]() <t≤2时,如图5,
<t≤2时,如图5,
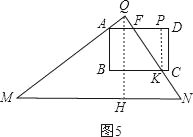
∵AD∥MN,
∴△QAF∽△QMN,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AF=11﹣5.5t,
过K作KP⊥AD于P,
则△KPF∽△QHN,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PF=1.5,
∴BK=AP=AF+PF=11﹣5.5t+1.5=12.5﹣5.5t,
∴S=![]() (AF+BK)CD=
(AF+BK)CD=![]() [11﹣5.5t+12.5﹣5.5t]×3,
[11﹣5.5t+12.5﹣5.5t]×3,
S=﹣![]() t+35.25.
t+35.25.

 名校课堂系列答案
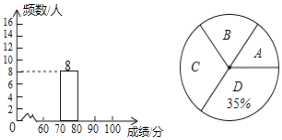
名校课堂系列答案【题目】某市为加强学生的安全意识,组织了全市学生参加安全知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示,请根据图表信息解答以下问题.
组别 | 成绩x/分 | 频数 |
A组 |
| a |
B组 |
| 8 |
C组 |
| 12 |
D组 |
| 14 |
(1)一共抽取了_____个参赛学生的成绩;表中![]() ____;
____;
(2)补全频数分布直方图;
(3)计算扇形统计图中“C”对应的圆心角度数;
(4)某校共有2000人,安全意识不强的学生(指成绩在70分以下)估计有多少人?