Question

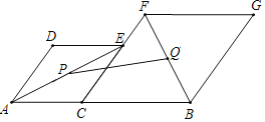
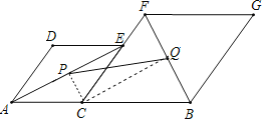
【题目】如图，已知AB＝2，C为线段AB上的一个动点，分别以AC，CB为边在AB的同侧作菱形ACED和菱形CBGF，点C，E，F在一条直线上，∠D＝120°．P、Q分别是对角线AE，BF的中点，当点C在线段AB上移动时，点P，Q之间的距离最短为_____（结果保留根号）．

Answer 1

【答案】．

【解析】

连接PC、CQ．首先证明∠PCQ＝90°，设AC＝2a，则BC＝﹣2a，PC＝a，CQ＝BC＝，利用勾股定理即可解决问题.

解：连接PC、CQ．

∵四边形ACED，四边形CBGF是菱形，∠D＝120°，

∴∠ACE＝120°，∠FCB＝60°，

∵P，Q分别是对角线AE，BF的中点，

∴∠ECP＝∠ACE，∠FCQ＝∠BCF，

∴∠PCQ＝90°，

设AC＝2a，则BC＝﹣2a，PC＝a，CQ＝BC＝

∴PQ＝

∴当a＝时，点P，Q之间的距离最短，最短距离是 ．

故答案为：．