Question

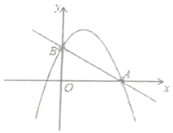
【题目】如图，已知二次函数的图像与轴的一个交点为，与轴的交点为，过，的直线为．点在轴上，当是等腰三角形时求出的坐标_____．

Answer 1

【答案】；；；

【解析】

把A点坐标代入求出c得到B(0，3)，则AB=5，设P(t，0)，讨论：当BP=BA时，P点与A点关于y轴对称，易得此时P点坐标；当AP=AB时，|t-4|=5，解绝对值方程求出t得到此时P点坐标；当PA=PB时，根据两点间的距离公式得到t2+32=(t-4)2，解方程求出t得到此时P点坐标．

把A(4，0)代入得，
解得：c=3，
则B(0，3)，
∴AB=，

设P(t，0)，
当BP=BA时，P点与A点关于y轴对称，此时P点坐标为(-4，0)，
当AP=AB时，|t-4|=5，解得：t=-1或t=9，

此时P点坐标为(-1，0)，(9，0)；
当PA=PB时，，即，

解得：t=，此时P点坐标为(，0)，
综上所述，P点坐标为(-4，0)，(-1，0)，(9，0)，(，0)．
故答案为：(-4，0)，(-1，0)，(9，0)，(，0)．