题目内容
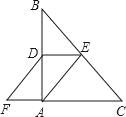
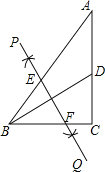
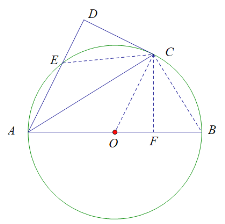
【题目】如图，AB为⊙O的直径，C为⊙O上一点，过点C做⊙O 的切线，与AE的延长线交于点D，且AD⊥CD．
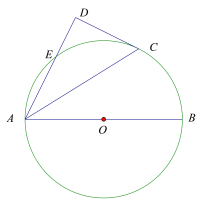
（1）求证：AC平分∠DAB；
（2）若AB=10，CD=4，求DE的长．
【答案】（1）见解析；（2）DE=2
【解析】
（1）连接OC，利用切线的性质可得出OC∥AD，再根据平行线的性质得出∠DAC=∠OCA，又因为∠OCA=∠OAC，继而可得出结论；
（2）方法一：连接BE交OC于点H，可证明四边形EHCD为矩形，再根据垂径定理可得出
，得出
，从而得出
，再通过三角形中位线定理可得出
，继而得出结论
；方法二：连接BC、EC，可证明△ADC∽△ACB，利用相似三角形的性质可得出AD=8，再证△DEC∽△DCA，从而可得出结论；方法三：连接BC、EC，过点C做CF⊥AB，垂足为F，利用已知条件得出OF=3，再证明△DEC≌△CFB，利用全等三角形的性质即可得出答案．
解：（1）证明：连接OC，
∵CD切☉O于点C
∴OC⊥CD
∵AD⊥CD
∴∠D=∠OCD=90°
∴∠D+∠OCD=180°
∴OC∥AD
∴∠DAC=∠OCA
∵OA=OC
∴∠OCA=∠OAC
∴∠DAC=∠OAC
∴AC平分DAB
（2）方法1：连接BE交OC于点H
∵AB是☉O直径
∴∠AEB=90°
∴∠DEC=90°
∴四边形EHCD为矩形
∴CD=EH=4
DE=CH
∴∠CHE=90°
即OC⊥BH
∴EH=BE=4
∴BE=8
∴在Rt△AEB中
AE
=6
∵EH=BH
AO=BO
∴OH=
AE=3
∴CH=2
∴DE=2
方法2：
连接BC、EC
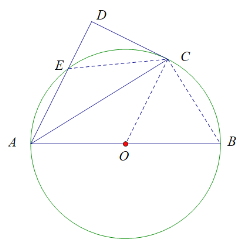
∵AB是直径
∴∠ACB=90°
∴∠D=∠ACB
∵∠DAC=∠CAB
∴△ADC∽△ACB
∴
∠B=∠DCA
∴AC2=10·AD
∵AC2=AD2+CD2
∴10·AD=AD2+16
∴AD=2舍AD=8
∵四边形ABCE内接于☉O
∴∠B+∠AEC=180°
∵∠DEC+∠AEC=180°
∴∠B=∠DEC
∴∠DEC=∠DCA
∵∠D=∠D
∴△DEC∽△DCA
∴
∴CD2=AD·DE
∴16=8·DE
∴DE=2；
方法3：
连接BC、EC，过点C做CF⊥AB，垂足为F
∵CD⊥AD，∠DAC=∠CAB
∴CD=CF=4，∠D=∠CFB=90°
∵AB=10
∴OC=OB=5
∴OF=3
∴BF=OB-OF=5-3=2
∵四边形ABCE内接于☉O
∴∠B+∠AEC=180°
∵∠DEC+∠AEC=180°
∴∠B=∠DEC
∴△DEC≌△CFB
∴DE=FB=2．
