题目内容
【题目】如图,在平面直角坐标系中,点P是以C![]() 为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最大值是________.
为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最大值是________.
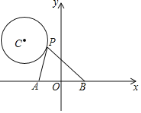
【答案】34
【解析】
设点P的坐标为(x,y),用含x,y的式子表示出PA2+PB2值,从而转化为求OP的最值,画出图形后可直观得出当OP经过圆心时,OP的值最大,代入求解即可.
解:设点P的坐标为(x,y),
又A(﹣1,0),B(1,0),
则PA2=(1+x)2+y2,PB2=(-x+1)2+y2,OP2=x2+y2,
∴PA2+PB2=(1+x)2+y2+(-x+1)2+y2=2(x2+y2)+2=2OP2+2,
当OP通过圆心时,∵OP2=OC+CP2= OC+CP1>OP1,
即P在P2点时,OP最大,即PA2+PB2最大,如图,

又OC=![]() ,
,
∴OP2=OC+CP2=3+1=4,
∴PA2+PB2的最大值=2OP22+2=2×42+2=34.
故答案为:34.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目