题目内容
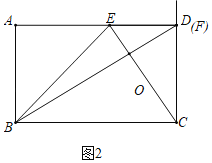
【题目】如图,已知在矩形ABCD中,AD=8,CD=4,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,到达A点停止运动;同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,到达D点停止运动,设点E移动的时间为t(秒).
(1)当t=1时,求四边形BCFE的面积;
(2)设四边形BCFE的面积为S,求S与t之间的关系式,并写出t的取值范围;
(3)若F点到达D点后立即返回,并在线段CD上往返运动,当E点到达A点时它们同时停止运动,求当t为何值时,以E,F,D三点为顶点的三角形是等腰三角形,并求出此的等腰三角形的面积S△EDF.

【答案】(1)S四边形BCFE=17;(2)S=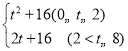 ;(3)当t=
;(3)当t=![]() 时,S△DEF=
时,S△DEF=![]() .当t=4时,S△DEF=8.
.当t=4时,S△DEF=8.
【解析】
(1)如图1中,t=1时,DE=1,CF=2,根据S四边形BCFE=S△BCE+S△ECF计算即可.
(2)分两种情形:如图1中,当0≤t≤2时,如图2中,当2<t≤8时,分别求解即可解决问题.
(3)由题意当DE=DF时,△DEF是等腰直角三角形.分两种情形分别构建方程解决问题即可.
解:(1)如图1中,
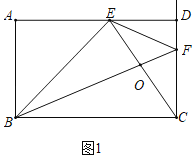
t=1时,DE=1,CF=2,
∴S四边形BCFE=S△BCE+S△ECF=![]() ×8×4+
×8×4+![]() ×2×1=17.
×2×1=17.
(2)如图1中,当0≤t≤2时,S=S△BCE+S△ECF=![]() ×8×4+
×8×4+![]() ×2t×t=t2+16.
×2t×t=t2+16.
如图2中,当2<t≤8时,S=S△BCE+S△EDC=![]() ×8×4+
×8×4+![]() ×4×t=2t+16.
×4×t=2t+16.
综上所述,S=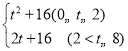 .
.
(3)由题意当DE=DF时,△DEF是等腰直角三角形.
可得4﹣2t=t或2t﹣4=t,
解得t=![]() 或4.
或4.
当t=![]() 时,S△DEF=
时,S△DEF=![]() ×
×![]() ×
×![]() =
=![]() .
.
当t=4时,S△DEF=![]() ×4×4=8.
×4×4=8.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目