题目内容
如图,在直角坐标系中,四边形OABC为矩形,A(8,0),C(0,6),点M是OA的中点,P、Q两点同时从点M出发,点P沿x轴向右运动;点Q沿x轴先向左运动至原点O后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度均为每秒1个单位.以P Q为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与矩形OABC重叠部分(阴影部分)的面积为S(平方单位).
Q为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与矩形OABC重叠部分(阴影部分)的面积为S(平方单位).
(1)用含t的代数式表示点P的坐标;
(2)分别求当t=1,t=5时,线段PQ的长;
(3)求S与t之间的函数关系式;
(4)连接AC.当正方形PRLQ与△ABC的重叠部分为三角形时,直接写出t的取值范围.
解:(1)∵MP=t,OM=4,
∴OP=t+4,
∴P(t+4,0)(0≤t≤8).
(2)当t=1时,PQ=2×1=2.
当t=5时,OP=9,OQ=5-4=1,
∴PQ=9-1=8.
(3)如图①,当0≤t≤3时,
∵PQ=2t,
∴S=4t2.
如图②,当3<t≤4时,
∵PQ=2t,AB=6,
∴S=12t.
如图③,当4<t≤8时,
∵AQ=4-(t-4)+4=12-t,AB=6,
∴S=-6t+72.

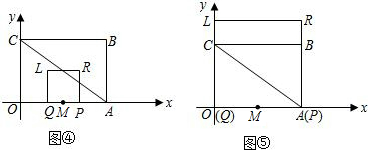
(4)如图④,当点R在AC上时,如图6,

∵RP∥OC,
∴△APR∽△AOC,
∴ =
= ,
,
∴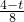 =
=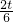 ,
,
∴t=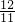 .
.
当点L在AC上时,如图7,

同理得出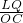 =
= ,
,
∴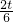 =
=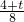 ,
,
t= ,
,
∴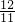 <t≤
<t≤ .
.
如图⑤,当点L在y轴上时,t=4.
分析:(1)点P的纵坐标一定为0,横坐标再4的基础上随时间的增加每秒增加1个单位,所以t秒后的坐标是(4+t,0);
(2)当t<4时,线段PQ的长为2t,当t>4时,线段PQ的长固定不变是8;
(3)分三种情况讨论:当t<4时,s=4t2,当t=4时,s=48,当t>4时,s=(8-t2);
(4)结合一次函数与题意直接写出t的取值范围.
点评:本题主要考查了矩形的性质、正方形的性质以及坐标与图形的性质的综合题,注意仔细审题,考虑要全面.
∴OP=t+4,
∴P(t+4,0)(0≤t≤8).
(2)当t=1时,PQ=2×1=2.
当t=5时,OP=9,OQ=5-4=1,
∴PQ=9-1=8.
(3)如图①,当0≤t≤3时,
∵PQ=2t,
∴S=4t2.
如图②,当3<t≤4时,
∵PQ=2t,AB=6,
∴S=12t.
如图③,当4<t≤8时,
∵AQ=4-(t-4)+4=12-t,AB=6,
∴S=-6t+72.

(4)如图④,当点R在AC上时,如图6,

∵RP∥OC,
∴△APR∽△AOC,
∴
 =
= ,
,∴
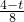 =
=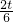 ,
,∴t=
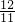 .
.当点L在AC上时,如图7,

同理得出
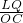 =
= ,
,∴
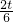 =
=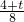 ,
,t=
 ,
,∴
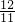 <t≤
<t≤ .
.如图⑤,当点L在y轴上时,t=4.

分析:(1)点P的纵坐标一定为0,横坐标再4的基础上随时间的增加每秒增加1个单位,所以t秒后的坐标是(4+t,0);
(2)当t<4时,线段PQ的长为2t,当t>4时,线段PQ的长固定不变是8;
(3)分三种情况讨论:当t<4时,s=4t2,当t=4时,s=48,当t>4时,s=(8-t2);
(4)结合一次函数与题意直接写出t的取值范围.
点评:本题主要考查了矩形的性质、正方形的性质以及坐标与图形的性质的综合题,注意仔细审题,考虑要全面.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

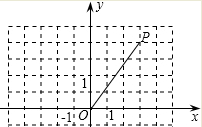 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: