题目内容
【题目】如图,将长方形纸片的一角作折叠,使顶点![]() 落在
落在![]() 处,
处,![]() 为折痕,将
为折痕,将![]() 对折,使得
对折,使得![]() 落在直线
落在直线![]() 上,得折痕
上,得折痕![]() ,若
,若![]() 恰好平分
恰好平分![]() ,则
,则![]() ___________
___________![]() .
.
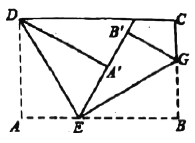
【答案】60°
【解析】
根据折叠的性质得到∠AED=∠A′ED,∠BEG=∠B′EG,再根据平角的定义得到∠AED+∠A′ED+∠BEG+∠B′EG=180°,即可得到∠DEG的度数再根据角平分线的定义和平角的定义即可得到结论.
∵长方形纸片的一角折叠,顶点A落在A′处,另一角折叠,顶点B落在EA′上的B′点处,
∴∠AED=∠A′ED,∠BEG=∠B′EG,
而∠AED+∠A′ED+∠BEG+∠B′EG=180°,
∴∠A′ED+∠B′EG=90°,即∠DEG=90°;
∵∠AED=∠A′ED,
∵EA′平分∠DEB,
∴∠A′ED=∠A′EB,
∴∠AED=∠DEA′=∠A′EB=![]() ×180°=60°,
×180°=60°,
故∠DEA′=60°.

 阅读快车系列答案
阅读快车系列答案【题目】“元且”期间,某校组织开展“班际歌泳比赛”,甲、乙班共有学生102人(其中甲班人数多于乙班人数,且甲班人数不够100人)报名统一购买服装参加演出.下面是某服装厂给出的演出服装的价格表:
购买服装的套数 | 1~50 | 51~100 | ≥101 |
每套服装的价格/元 | 70 | 60 | 50 |
如果两班分别单独购买服装,总共要付款6580元
(1)如果甲、乙两班联合起来购买服装,那么比各自购买服装总共可以节省多少钱?
(2)甲、乙班各有多少学生报名参加比赛?
(3)如果甲班有5名学生因特殊情况不能参加演出,请你为两班设计一种省钱的购买服装方案.
【题目】某校为了解同学们课外阅读名著的情况,在八年级随机抽查了20名学生,调查结果如表所示:
课外名著阅读量(本) | 8 | 9 | 10 | 11 | 12 |
学生人数 | 3 | 3 | 4 | 6 | 4 |
关于这20名学生课外阅读名著的情况,下列说法错误的是( )
A.中位数是10B.平均数是10.25C.众数是11D.阅读量不低于10本的同学点70%