Question

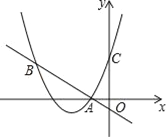
【题目】如图，二次函数y=（x+2）2+m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y=kx+b的图象经过该二次函数图象上的点A（﹣1，0）及点B．

（1）求二次函数与一次函数的解析式；

（2）根据图象，写出满足（x+2）2+m≥kx+b的x的取值范围．

Answer 1

【答案】（1）抛物线解析式为y=x2+4x+3，一次函数解析式为y=﹣x﹣1；（2）由图象可知，满足（x+2）2+m≥kx+b的x的取值范围为x﹣4或x≥﹣1．

【解析】（1）先利用待定系数法先求出m，再求出点B坐标，利用方程组求出太阳还是解析式．

（2）根据二次函数的图象在一次函数的图象上面即可写出自变量x的取值范围．

解：（1）∵抛物线y=（x+2）2+m经过点A（﹣1，0），∴0=1+m，∴m=﹣1，∴抛物线解析式为y=（x+2）2﹣1=x2+4x+3，∴点C坐标（0，3），∵对称轴x=﹣2，B、C关于对称轴对称，∴点B坐标（﹣4，3），∵y=kx+b经过点A、B，

∴，解得，

∴一次函数解析式为y=﹣x﹣1，

（2）由图象可知，写出满足（x+2）2+m≥kx+b的x的取值范围为x＜﹣4或x＞﹣1．