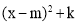题目内容
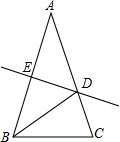
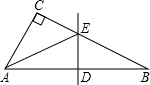
如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,∠CAE:∠EAB=4:1,求∠B的度数.

∵△ABC中,∠ACB=90°,DE是AB的垂直平分线,
∴∠EAB=∠ABE,
∵∠CAE:∠EAB=4:1,设∠EAB=x,则∠CAE=4x,
∵∠ABE+∠CAE+∠EAB=90°,即4x+x+x=90°,
解得:x=15°,
∴∠B=x=15°.
∴∠EAB=∠ABE,
∵∠CAE:∠EAB=4:1,设∠EAB=x,则∠CAE=4x,
∵∠ABE+∠CAE+∠EAB=90°,即4x+x+x=90°,
解得:x=15°,
∴∠B=x=15°.

练习册系列答案
相关题目