Question

【题目】如图所示，已知AB为⊙O的直径，CD是弦，且AB⊥CD于点E，连接AC、OC、BC

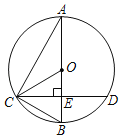
（1）求证：∠ACO＝∠BCD；

（2）若EB＝8cm，CD＝24cm，求⊙O的面积．（结果保留π）

Answer 1

【答案】（1）见解析；（2）169π（cm2）．

【解析】

（1）根据垂径定理，即可得＝，根据同弧所对的圆周角相等，证出∠BAC＝∠BCD，再根据等边对等角，即可得到∠BAC＝∠ACO，从而证出∠ACO＝∠BCD；

（2）根据垂径定理和勾股定理列出方程，求出圆的半径，即可求出圆的面积.

解：（1）∵AB为⊙O的直径，AB⊥CD，

∴＝．

∴∠BAC＝∠BCD．

∵OA＝OC，

∴∠BAC＝∠ACO．

∴∠ACO＝∠BCD；

（2）∵AB为⊙O的直径，AB⊥CD，

∴CE＝CD＝×24＝12（cm）．

在Rt△COE中，设CO为r，则OE＝r﹣8，

根据勾股定理得：122+（r﹣8）2＝r2

解得r＝13．

∴S⊙O ＝π×132＝169π（cm2）．